Enunciado
Álgebra Linear e Geometria Analítica - Um curso de geometria analítica e álgebra linear, Reginaldo J. Santos- Ed: 1º - Capítulo 5.4 - Ex. 1a
Encontre as coordenadas do ponto com relação ao sistema de coordenadas , nos seguintes casos:
a)
Passo 1
Oiii, como vai? Tudo certinho?
Para esta questão vamos precisar relembrar como que fazemos uma mudança de coordenadas em uma notação matricial, saca só:
em que é a base ortonormal do novo sistema de coordenadas, é a base canônica, e a matriz (as colunas são formadas pelos vetores de base do novo sistema de coordenadas). Vamos aplicar esta definição então!
Passo 2
Temos de cada substituindo os dados do enunciado que:
Realizando o produto matricial, temos que
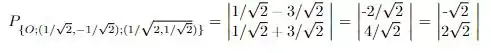
Está aí o nosso ponto, nas novas coordenadas! Essa alternativa já foi, vamos para a próxima!
Resposta
Ao longo dos passos.
Exercícios de Livros Relacionados
Nos Exercícios 17-20, encontre a solução geral do sistema linear e confirme que os vetores linha da matriz de coeficientes são ortogonais aos vetores solução.17. x 1 + x 2 + x 3 = 0 2 x 1 + 2 x 2 + 2
21.(a) A equação x + y + z = 1 pode ser vista como um sistema linear de uma equação em três incógnitas. Expresse uma solução geral dessa equação como uma solução particular somada com uma solução gera
Nos Exercícios 17-20, encontre a solução geral do sistema linear e confirme que os vetores linha da matriz de coeficientes são ortogonais aos vetores solução.18. x 1 + 3 x 2 - 4 x 3 = 0 2 x 1 + 6 x 2
Nos Exercícios 27-28, encontre uma solução geral do sistema e use essa solução para encontrar uma solução geral do sistema homogêneo associado e uma solução particular do sistema dado. 27. 3 4 1 2 6 8
Nos Exercícios 17-20, encontre a solução geral do sistema linear e confirme que os vetores linha da matriz de coeficientes são ortogonais aos vetores solução.20. x 1 + 3 x 2 - 4 x 3 = 0x 1 + 2 x 2 + 3