Enunciado
Álgebra Linear e Geometria Analítica - Um curso de geometria analítica e álgebra linear, Reginaldo J. Santos- Ed: 1º - Capítulo 5.4 - Ex. 1b
Encontre as coordenadas do ponto com relação ao sistema de coordenadas , nos seguintes casos:
b)
Passo 1
O processo é basicamente o mesmo que o da alternativa anterior, a diferença é que agora estamos no , então vamos com calma! Beleza?
Passo 2
Usando os dados do enunciado temos que
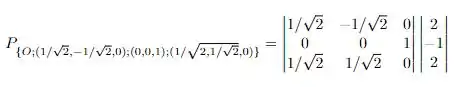
Realizando o produto matricial, temos que
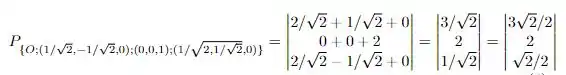
Está aí o nosso ponto, nas novas coordenadas! A questão é isso, te vejo na próxima!
Resposta
Ao longo dos passos.
Exercícios de Livros Relacionados
Nos Exercícios 1-4, encontre as equações vetoriais e paramétricas da reta contendo o ponto e paralela ao vetor.4. Ponto: - 9 , 3 , 4 ; vetor: v = ( - 1 , 6 , 0 )
Nos Exercícios 9-12, encontre as equações vetoriais e paramétricas do plano contendo o ponto e paralelo aos vetores.12. Ponto: 0 , 5 , - 4 ; vetores: v 1 = 0 , 0 ,- 5 e v 2 = 1 ,- 3 ,2
Nos Exercícios 1-4, encontre as equações vetoriais e paramétricas da reta contendo o ponto e paralela ao vetor.3. Ponto: 0 , 0,0 ; vetor: v = ( - 3 , 0,1 )
Nos Exercícios 5-8, use a equação da reta dada para encontrar um ponto na reta e um vetor paralelo à reta.7. x = 1 - t 4,6 + t - 2,0
Nos Exercícios 13-14, encontre as equações vetoriais e paramétricas da reta em R 2 que passa pela origem e é ortogonal a v .13. v = 1 , - 4