Enunciado
Álgebra Linear e Geometria Analítica - Álgebra Linear - 2ª Edição - Alfredo Steinbruch e Paulo Winterle- Ed: 2º - Capítulo 7.5 - Ex. 29
A equação representa uma cônica degenerada. Identificá-la e esboçar o gráfico, quando possível.
Passo 1
Aqui a gente não tem muito o que arrumar, só fechar o quadrado perfeito que já tá na nossa cara!
Tirando o quadrado:
Com o sinal de :
Com o sinal de :
Passo 2
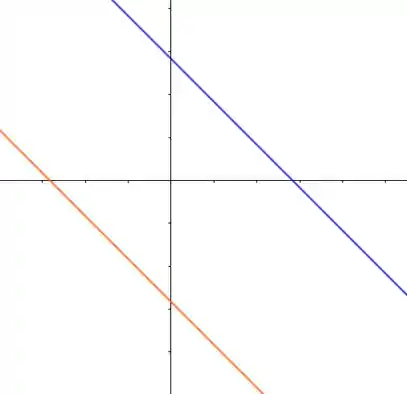
Essas duas equações que encontramos representam duas retas paralelas! Esboçando:
Resposta
Duas retas paralelas:
Exercícios de Livros Relacionados
Nos exercícios de 5 a 12, remova da equação dada o termo x y por uma rotação de eixos. Faça um esboço do gráfico e mostre os dois conjuntos de eixos. 6 . 4 x y + 3 x 2 = 4
Nos exercícios de 5 a 12, remova da equação dada o termo x y por uma rotação de eixos. Faça um esboço do gráfico e mostre os dois conjuntos de eixos. 8 . x 2 + x y + y 2 = 3
Nos exercícios de 5 a 12, remova da equação dada o termo x y por uma rotação de eixos. Faça um esboço do gráfico e mostre os dois conjuntos de eixos. 7 . x 2 + 2 x y + y 2 - 8 x + 8 y = 0
Nos exercícios de 5 a 12, remova da equação dada o termo x y por uma rotação de eixos. Faça um esboço do gráfico e mostre os dois conjuntos de eixos. 9 . x y + 16 = 0
Nos exercícios de 5 a 12, remova da equação dada o termo x y por uma rotação de eixos. Faça um esboço do gráfico e mostre os dois conjuntos de eixos. 10 . 5 x 2 + 6 x y + 5 y 2 = 9