Enunciado
Álgebra Linear e Geometria Analítica - Álgebra Linear - 2ª Edição - Alfredo Steinbruch e Paulo Winterle- Ed: 2º - Capítulo 7.5 - Ex. 34
A equação representa uma cônica degenerada. Identificá-la e esboçar o gráfico, quando possível.
Passo 1
Essa expressão é do tipo que a gente conhece como “homogênea”. Ela é chamada assim porque todos os termos têm o mesmo grau, se ligou? é de grau , é de grau e é de grau . Sacou? A idéia nessas expressões é a gente a expressão toda por uma das letras, assim:
Divide tudo por :
Mas ó, isso aí a gente faz considerando que o já é diferente de , porque não podemos dividir por , beleza? Depois a gente vai ter que analisar o caso de pra ver se tinha solução.
Passo 2
Pra resolver essa equação, vamos chamar de :
Equação do segundo grau a gente sabe resolver!
Ih rapaz, número complexo não é pra gente não! Aqui a gente só mexe com número real. Se não tem solução real, vamos dizer que o conjunto não representa nenhum ponto do plano!
Passo 3
Mas galera, falta a gente analisar o caso do , né? Vamos dar uma olhada nesse caso, substituindo na expressão original.
Opa, então na real tem um ponto sim! O ponto serve pra gente, mas só ele! Ainda bem que não esquecemos desse caso!
Passo 4
A representação gráfica dele é:
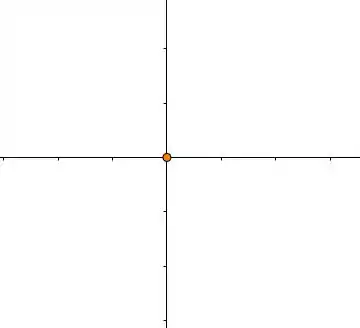
Resposta
Ponto .