Enunciado

Álgebra Linear e Geometria Analítica - Álgebra Linear - 3ª Edição - J. L. Boldrini- Ed: 3º - Capítulo 11.7.2 - Ex. 1d

Esboce o gráfico das cônicas a seguir, determinando seus focos, diretrizes e excentricidade.

Passo 1

Nesse caso, temos uma elipse especial, onde . Quando isso acontece, temos uma circunferência! Repare:

Isso é o mesmo que o conjunto de todos os pontos que distam da origem; ou seja, o raio da nossa circunferência é .

Passo 2

Nossa circunferência de raio fica o seguinte:

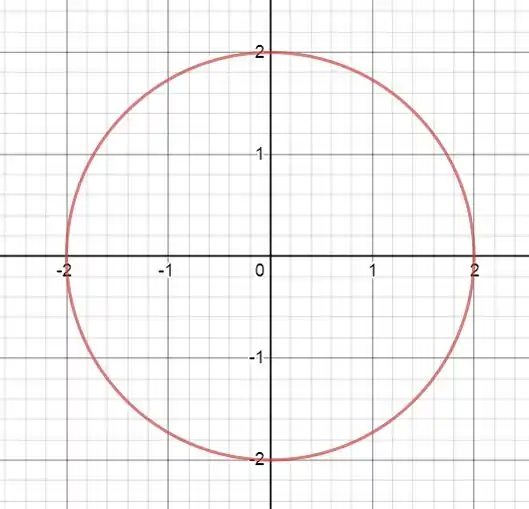
Passo 3

Os conceitos de foco e excentricidade tem uma interpretação interessante na circuinferencia! Se seguirmos a fórmula dos focos de uma elipse normalmente:

O que quer dizer que nossos focos estão no mesmo ponto: que é exatamente o centro da circunferência! Podemos ver uma circunferência como uma elipse de um foco só. Para a excentricidade, temos:

E por definição, a circunferência não tem diretriz.

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em cada um dos problemas de 1 a 12 , esboçar o gráfico e determinar os vértices, os focos, a excentricidade e as equações das assíntotas das hipérboles dadas.1. x 2 4 - y 2 9 = 1

Em cada um dos problemas de 1 a 12 , esboçar o gráfico e determinar os vértices, os focos, a excentricidade e as equações das assíntotas das hipérboles dadas.8. x 2 - y 2 = 1

Em cada um dos problemas de 1 a 12 , esboçar o gráfico e determinar os vértices, os focos, a excentricidade e as equações das assíntotas das hipérboles dadas.5. 4 x 2 - 5 y 2 + 20 = 0

Em cada um dos problemas de 1 a 12 , esboçar o gráfico e determinar os vértices, os focos, a excentricidade e as equações das assíntotas das hipérboles dadas.7. x 2 - 4 y 2 + 16 = 0

Em cada um dos problemas de 1 a 12 , esboçar o gráfico e determinar os vértices, os focos, a excentricidade e as equações das assíntotas das hipérboles dadas.10. y 2 - 4 x 2 = 1