Enunciado
Álgebra Linear e Geometria Analítica - Álgebra Linear - 3ª Edição - J. L. Boldrini- Ed: 3º - Capítulo 11.7.2 - Ex. 1g
Esboce o gráfico das cônicas a seguir, determinando seus focos, diretrizes e excentricidade.
Passo 1
Como os dois termos têm sinais diferentes, a cônica que estamos analisando é uma hipérbole! Ela já tá quase da forma canônica, só falta explicitar o e o .
No nosso caso, e .
Passo 2
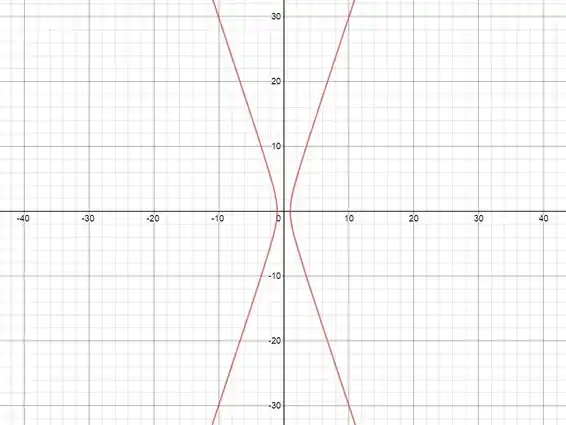
Esboçando a cônica, ficamos com essa hipérbole bem íngreme:
Passo 3
Para os deus pontos focais, teremos:
Onde
Para sua excentricidade:
E finalmente, suas diretrizes:
Resposta
Exercícios de Livros Relacionados
13. Esboçar o gráfico de uma hipérbole (com suas assíntotas) de centro 0 ,0 , eixo real sobre O x e excentricidade:b) 3 2
Em cada um dos problemas de 1 a 12 , esboçar o gráfico e determinar os vértices, os focos, a excentricidade e as equações das assíntotas das hipérboles dadas.3. 16 x 2 - 25 y 2 - 400 = 0
Em cada um dos problemas de 1 a 12 , esboçar o gráfico e determinar os vértices, os focos, a excentricidade e as equações das assíntotas das hipérboles dadas.9. y 2 - x 2 = 2
13. Esboçar o gráfico de uma hipérbole (com suas assíntotas) de centro 0 ,0 , eixo real sobre O x e excentricidade:a) 5 3
Usando coordenadas polares r ,θ no plano ( x = r cos θ ,y = rs e nθ ) e a definição de cônica dada por 11.7.4, parte 3, você pode deduzir de modo simples as equações polares das cônicas, tomando o p