Em cada um dos problemas de a , esboçar o gráfico e determinar os vértices, os focos, a excentricidade e as equações das assíntotas das hipérboles dadas.
7.
Passo 1
Então galera, antes de começarmos com a resolução devemos extrair duas informações sobre a equação que nos foi dada, que são os fatores e da equação! Mas que fatores são esses? Então, de acordo com o que estudamos a equação de uma hipérbole pode ter dois formatos:
Ou:
A equação que nos foi dada é essa aqui:
Simplificando para escrevermos no formato padrão:
Que condiz com o segundo formato, certo? Então se compararmos os denominadores, teremos:
Ok, encontramos e ! Agora podemos iniciar a resolução de fato, então bora lá!
Passo 2
Para encontrarmos os vértices da hipérbole é de boa! Nesse caso eles são dados pelos pontos:
Como , então nossos vértices serão:
Ademais, para encontrarmos os focos da hipérbole também é bem tranquilão, galera! Basta que encontremos o da nossa equação utilizando o Teorema de Pitágoras, pois os focos, para a equação nesse formato, são dados pelos pontos:
Aplicando o Teorema:
Então nossos focos serão:
Show! Metade do caminho foi concluído, agora vamos para o final!
Passo 3
A excentricidade de uma hipérbole é dada pela seguinte razão:
Substituindo os valores, teremos:
Por fim, para determinarmos as equações das assíntotas, temos que utilizar as relações:
Substituindo os valores, teremos:
Esboçando essa hipérbole, teremos o seguinte, galera:
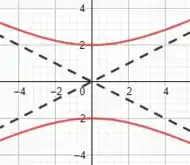
No qual as curvas em vermelho é a hipérbole e as linhas tracejadas em preto são as assíntotas. E está aí nossa resolução!
Resposta