Enunciado
Álgebra Linear e Geometria Analítica - LIMA, Elon L. Geometría analítica e Álgebra Linear- Ed: 2º - Capítulo 5.Problemas - Ex. 4
Escolhendo um sistema de coordenadas com origem no vértice A e com o ponto B sobre o eixo das abcissas, prove que as três medianas de um triângulo se encontram no mesmo ponto, o qual divide cada uma delas na razão a partir do vértice correspondente.
Passo 1
Fala aí pessoal tudo blz?
Nessa questão um sistema de coordenadas com origem no vértice A e com o ponto B sobre o eixo das abcissas, prove que as três medianas de um triângulo se encontram no mesmo ponto, o qual divide cada uma delas na razão a partir do vértice correspondente.
Pode ficar calminho que você vai entender legal, só confia.
Passo 2
Sabendo que,
O sistema de coordenadas com origem no vértice e com o ponto sobre o eixo das abscissas
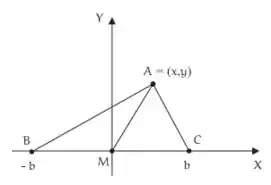
Ficando,
Sendo,
Espero ter ajudado, e até a próxima.
Resposta
Exercícios de Livros Relacionados
“Num triângulo retângulo, a altura relativa à hipotenusa é a média geométrica das projeções (ortogonais) dos catetos sobre essa hipotenusa.” Prove este fato escolhendo um sistema de coordenadas onde a
Dados os pontos A, B, determine o conjunto dos pontos do plano cuja soma dos quadrados de suas distâncias a A e B é igual a uma constante c.
Esboce o gráfico do conjunto das soluções de cada uma das desigualdades a seguir: x 2 + y 2 ≥ 1
Esboce o gráfico do conjunto das soluções de cada uma das desigualdades a seguir: y ≤ x 2