Enunciado
Álgebra Linear e Geometria Analítica - Um curso de geometria analítica e álgebra linear, Reginaldo J. Santos- Ed: 1º - Capítulo 4.1 - Ex. 2a
Faça um esboço das retas a seguir: a) .
Passo 1
E aí pessoal, belezinha? Vamos trabalhar agora em algumas questões de geometria analítica.
Para responder ao questionamento do enunciado, usamos a equação vetorial da reta para identificarmos o ponto P que pertence a esta, e o vetor diretor v, lembrando que:
Item a
Do que o item da questão nos fornece temos que:
Passo 2
Usando o Geogebra vamos esboçar a reta pedida.
Inicialmente abrimos a calculadora 3D:
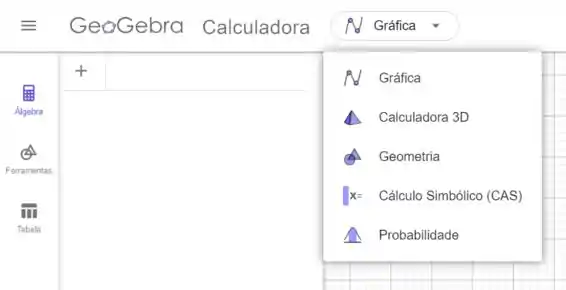
Inserimos o ponto P:
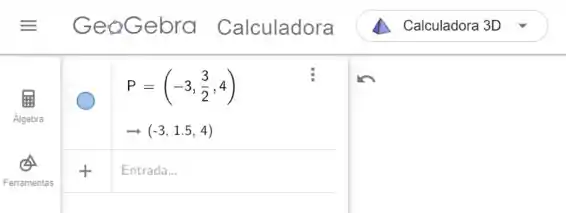
Inserimos o vetor v:
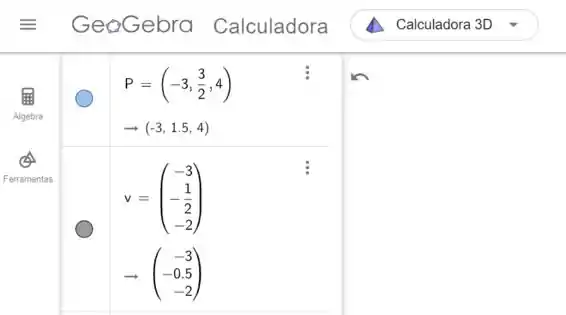
Em ferramentas clicamos em reta paralela:
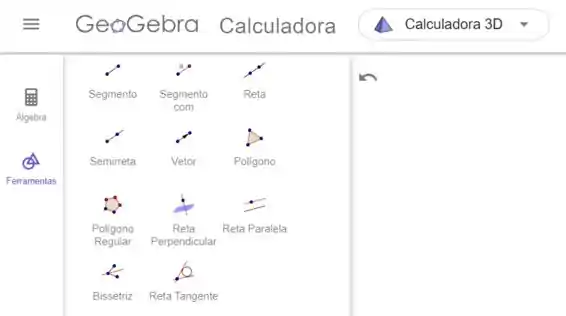
O software vai pedir um ponto e depois um vetor. Clicamos no ponto P, e depois no vetor diretor. E obteremos a reta desejada:
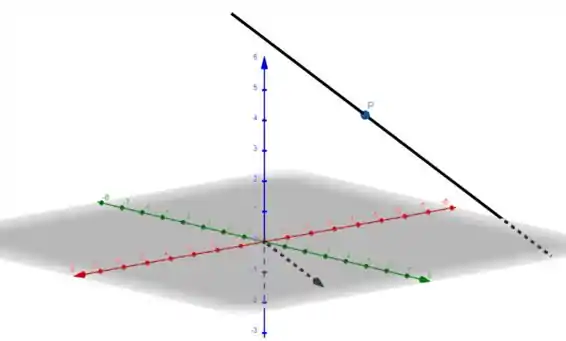
Resposta
Ver passo a passo.
Exercícios de Livros Relacionados
No quadrado ABCD, tem-se A = - 1 , - 3eB = ( 5,6 ) . Quais são as coordenadas dos vértices C e D?
O triângulo ABC, com A = - a , 0 ,B = a , 0eC = ( 0 , y ) é equilátero. Quais são os valores possíveis de y?
Sejam A 1,2eB = - 3 , - 4 . Qual é o ponto de abscissa 5 sobre a reta perpendicular a AB passando pelo ponto C = ( 5,6 ) ?
Ache a equação da perpendicular à reta y = 3 x - 1 baixada do ponto Q = ( 2,2 ) .
Sejam A = a , 0eB = 0 , b , com a b ≠ 0 . Escreva, sob a forma α x + β y = c , a equação da reta que contém a altura do triângulo retângulo OAB, baixada do vértice do ˆangulo reto sobre a hipotenusa