Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 9.Exercício - Ex. 33
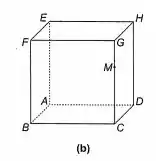
A Figura 9-4 (b) mostra um cubo. Sabendo que o comprimento de é o dobro do comprimento de , calcule a medida do ângulo .
Passo 1
Para simplificar bastante as contas, vamos adotar a base . Assim, as coordenadas dos pontos de interesse são:
A base escolhida é ortonormal, então podemos brincar com produto escalar!
Passo 2
O que queremos é o ângulo entre e . Desta forma, precisamos achar esses vetores:
Passo 3
Para achar o ângulo entre eles, usamos:
As normas são:
Já o produto escalar é
Portanto,
Logo,
Resposta
Exercícios de Livros Relacionados
Encontre um vetor unitário que tenha a mesma direção que o vetor dado:
Encontre um vetor a → com representação dada pela direção da linha A B → . Desenhe A B → e a representação equivalente a partir da origem.
Encontre um vetor a → com representação dada pela direção da linha A B → . Desenhe A B → e a representação equivalente a partir da origem.
Encontre um vetor a → com representação dada pela direção da linha A B → . Desenhe A B → e a representação equivalente a partir da origem.
Encontre um vetor a → com representação dada pela direção da linha A B → . Desenhe A B → e a representação equivalente a partir da origem.