Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 11.Exercício - Ex. 3
O triângulo tem área . Sabendo que e , calcule .
Passo 1
Esse problema explora o fato de a norma do produto vetorial ser igual a área do paralelogramo formado pelos dois vetores:
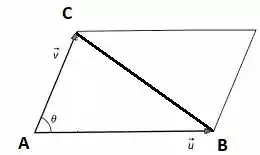
Nesse caso, e . Assim, é a área do paralelogramo desenhado.
Passo 2
Sabemos que a área do triângulo é metade da área do paralelogramo:
Portanto,
Resposta
Exercícios de Livros Relacionados
Mostrar que o quadrilátero cujos vértices são os pontos A 1 ,- 2 ,3 , B 4 ,3 ,- 1 , C ( 5 ,7 ,- 3 ) e D ( 2 ,2 ,1 ) é um paralelogramo e calcular sua área.
Dados os vetores u → = 2 ,1 ,0 e v → = ( 3 , - 6 ,9 ) , determinar o vetor x → que satisfaz a relação v → = u → × x → e que seja ortogonal ao vetor w → = ( 1 , - 2 ,3 ) .
Dado o triângulo de vértices A 0 ,1 , - 1 , B ( - 2 ,0 ,1 ) e C ( 1 , - 2 ,0 ) , calcular a medida da altura relativa ao lado B C .
Sejam u , v e w vetores não nulos com o mesmo ponto inicial no espaço tridimensional, mas tais que dois quaisquer não são colineares. Mostre que u × v × w está no plano determinado por u e v
Determine o produto vetorial a × b e verifique que ele é ortogonal a a e b .