Enunciado
Álgebra Linear e Geometria Analítica - Anton - Álgebra Linear- Ed: 10º - Capítulo 1.8 - Ex. 1
- A figura dada mostra uma rede na qual são conhecidos a taxa de fluxo e o sentido do fluxo em alguns ramos. Encontre as taxas de fluxo e os sentidos de fluxo nos demais ramos.
Passo 1
Assim como foi feito no exemplo 1, vamo adotar um sentido qualquer para o fluxo e calcular as taxas, se encontrarmos valores negativos quer dizer que adotamos o sentido errado para o fluxo.
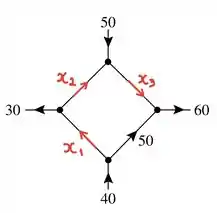
Passo 2
Agora vamos montar as equações para cada uma dos 4 nós:
Nó de cima:
Nó da direita:
Nó de baixo:
Nó da esquerda:
Passo 3
Dois dos fluxos já temos:
Então é só substituir em alguma das outras duas equações:
Ou seja, adotamos o sentido errado do fluxo e , já a direção do fluxo estava correta.
Resposta
Para os sentidos adotados:
Exercícios de Livros Relacionados
Em cada parte, encontre um seistema de equações lineares correspondente à matriz aumentada: 2 - 4 1 3- 1 - 6 - 1 0
Em cada parte, encontre a matriz aumentada do sistema de equações lineares dado: 2 x 2 - 3 x 4 + x 5 = 0 - 3 x 1 - x 2 + x 3 = - 1 6 x 1 + 2 x 2 - x 3 + 2 x 4 - 3 x 5 = 6
Em cada parte, encontre um seistema de equações lineares correspondente à matriz aumentada: 7 1 2 2 1 4 - 3 0 5 1
Em cada parte, encontre um seistema de equações lineares correspondente à matriz aumentada: 3 - 4 - 1 0 0 0 3 0 1 4 0 0 - 4 1 - 2 - 1 3 - 3 - 9 - 2
Em cada parte, encontre um seistema de equações lineares correspondente à matriz aumentada: 3 7 0 0 1 - 2 - 2 4 1 5 - 3 7