Enunciado
Álgebra Linear e Geometria Analítica - Álgebra Linear - 2ª Edição - Alfredo Steinbruch e Paulo Winterle- Ed: 2º - Capítulo 7.5 - Ex. 1r
Identificar as seguintes cônicas:
Passo 1
A questão pede para identificarmos a cônica cuja equação foi dada.
Neste caso, temos
Trata-de de um hipérbole cuja equação reduzida é
Temos e : o eixo real é o eixo !
Passo 2
Um esboço da cônica é dado a seguir:
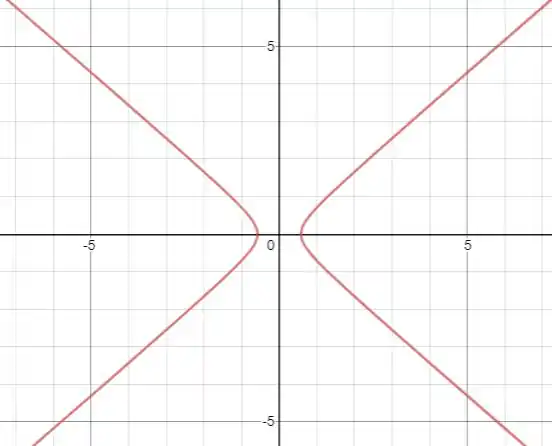
Resposta
Hipérbole
Exercícios de Livros Relacionados
Determinar a equação reduzida referida ao sistema X O ' Y e o gênero da cônica representada pela equação dada a seguir. Esboçar o gráfico. 7 x 2 - 8 x y + y 2 - 17 5 x + 11 5 y + 41 = 0
A equação representa uma cônica degenerada. Identificá-la e esboçar o gráfico, quando possível. x 2 + y 2 + 4 x y = 0
Efetuar uma rotação nos eixos coordenados a fim de eliminar o termo x y . Identificar a cônica e escrever sua equação no sistema x ' O y ' obtido após a rotação. Esboçar o gráfico. 3 x 2 + 2 x y + 3 y
Efetuar uma rotação nos eixos coordenados a fim de eliminar o termo x y . Identificar a cônica e escrever sua equação no sistema x ' O y ' obtido após a rotação. Esboçar o gráfico. 2 x 2 + 4 x y + 2 y
Efetuar uma rotação nos eixos coordenados a fim de eliminar o termo x y . Identificar a cônica e escrever sua equação no sistema x ' O y ' obtido após a rotação. Esboçar o gráfico. 2 x 2 + 2 6 x y + y