Se é uma matriz diagonal, então é igual a?
Passo 1
Primeiro vamos ver o que é uma matriz diagonal, ela é uma matriz quadrada onde os elementos onde , ou seja, todos os elementos que não estão na diagonal são nulos, como exemplo a matriz abaixo:
Passo 2
Agora a matriz é a matriz transposta de , e achamos essa matriz trocando as linhas pelas colunas da matriz , vamos então achar a matriz transposta de :
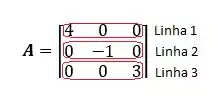
Vamos então colocar essas linhas no lugar das colunas:
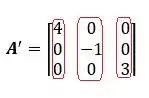
Pronto temos que a matriz é:
As matrizes são iguais!!
Assim vemos que toda matriz diagonal é simétrica, assim a matriz transposta de uma matriz diagonal é igual a própria matriz diagonal :