Enunciado
Álgebra Linear e Geometria Analítica - Alfredo Steinbruch e Paulo Winterle - Geometria Analítica- Ed: 1º - Capítulo 7.3.Problemas Propostos - Ex. 31e
Obter a equação reduzida resultante de uma translação de eixos, classificar, dar os elementos e representar graficamente as equações:
Passo 1
Vamos começar analisando a equação dada:
Aqui temos apenas um ao quadradado, indicando que se trata de uma parábola em . Isolando os termos em comum:
Completando os quadrados, teremos:
A equação de translação pode ser dada por:
Passo 2
A equação da parábola em é dada por:
E teremos :
Se a nossa equação é:
Então:
Outra coordenada que podemos determinar é e que acompanham e na equação:
Vamos agora calcular e :
Com isso, conseguimos esboçar o gráfico.
Passo 3
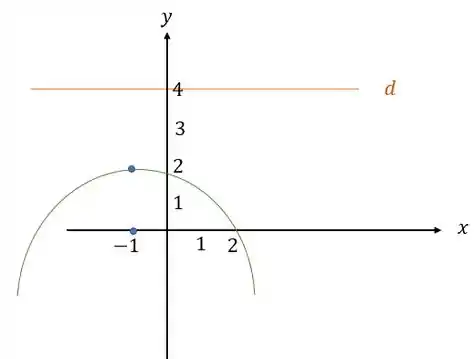
Resposta
, parábola, parábola , diretriz , )
Exercícios de Livros Relacionados
Para a parábola, ache as coordenadas do foco, a equação da diretriz e o comprimento do latus rectum. Faça um esboço da parábola. x 2 + y = 0
Ache uma equação da parábola com as propriedades dadas.Vértice ( 0 ,0 ) ; diretriz 2 x = - 5 .
Para a parábola, ache as coordenadas do foco, a equação da diretriz e o comprimento do latus rectum. Faça um esboço da parábola. y 2 = 6 x
Para a parábola, ache as coordenadas do foco, a equação da diretriz e o comprimento do latus rectum. Faça um esboço da parábola. 3 x 2 + 4 y = 0
Ache a equação da parábola que tem vértice na origem, eixo no eixo x e passa pelo ponto ( 2 ,- 4 ) .