Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Alfredo Steinbruch e Paulo Winterle - Geometria Analítica- Ed: 1º - Capítulo 7.3.Problemas Propostos - Ex. 31a

Obter a equação reduzida resultante de uma translação de eixos, classificar, dar os elementos e representar graficamente as equações:

x 2 + 4 y 2 - 4 x - 24 y + 36 = 0

Passo 1

Vamos começar analisando a equação dada:

x 2 + 4 y 2 - 4 x - 24 y + 36 = 0

Aqui temos um x e um y ao quadradado, indicando que pode ser tratar tanto de uma hipérbole, quanto de uma elipse. Isolando os termos em comum:

x 2 - 4 x 2 + 4 y 2 - 24 y = - 36

Como tanto   x 2 e y 2 são positivos, o que temos aqui é uma elipse. Completando os quadrados, teremos:

x 2 - 4 x + 2 2 - 2 2 + 4 y 2 - 6 y + 3 2 - 3 2 = - 36

x 2 - 4 x + 4 - 4 + 4 y 2 - 6 y + 9 - 9.4 = - 36

x - 2 2 - 4 + 4 y - 3 2 - 36 = - 36

x - 2 2 + 4 y - 3 2 = 4

Dividindo tudo por 4:

x - 2 2 4 + 4 y - 3 2 4 = 4 4

x - 2 2 4 + y - 3 2 1 = 1

A equação de translação pode ser dada por:

x ' = ( x - 2 )

y ' = ( y - 3 )

x ' 2 4 + y ' 2 1 = 1

Passo 2

A equação da elipse é dada por:

x - h 2 a 2 + y - k 2 b 2 = 1

Nossa equação é:

x - 2 2 4 + y - 3 2 1 = 1

Podemos dizer que o Eixo Maior é dado por 2 a e o menor é dado por 2 b . Se:

a 2 = 4

a = 2

b 2 = b = 1

Então o eixo maior vale 4 e o menor vale 2.

Outra coordenada que podemos determinar é h e k que acompanham x e y na equação:

h = 2

k = 3

Além disso, conhecemos a e b , mas desconhecemos c . O teorema de Pitágoras de uma Elipse é dado por:

a 2 = c 2 + b 2

4 = c 2 + 1

c 2 = 3

c = 3

Vamos agora calcular F 1,2 ; A 1,2   e   B 1,2 :

A 1,2 = ( h ∓ a , k )

B 1,2 = ( h , k ∓ b )

F 1,2 = ( h ± c , k )

Então:

A 1 = ( 0,3 )

A 2 = ( 4,3 )

B 1 = ( 2,2 )

B 2 = ( 2,4 )

F = ( 2 ± 3 , 3 )

Passo 3

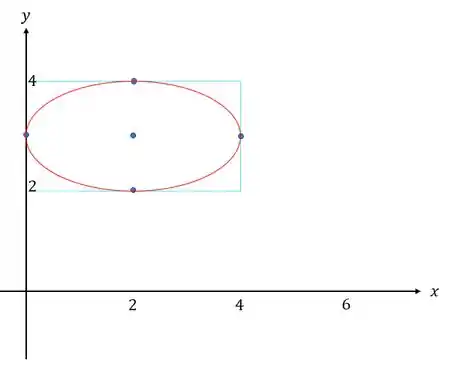
Resposta

x ' 2 4 + y ' 2 = 1 , elipse, eixo maior 4, eixo menor 2, focos F ( 2 ± 3 , 3 )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em cada um dos problemas 1 a 8, determinar os vértices A 1 e A 2 , os focos e as excentricidades das elipses dadas. Esboçar o gráfico.4) 9 x 2 + 5 y 2 - 4 5 = 0
Em cada um dos problemas 9 a 22, determinar a equação da elipse que satisfaz as condições dadas.14) vértices A ( 0 ,± 6 ) e passando pelo ponto P 3 ,2 .
Em cada um dos problemas 9 a 22, determinar a equação da elipse que satisfaz as condições dadas.16) eixo maior mede 10 e os focos F 1 ( 2 , - 1 ) e F 2 ( 2 ,5 ) .
Em cada um dos problemas 9 a 22, determinar a equação da elipse que satisfaz as condições dadas.12) centro C ( 0 ,0 ) , eixo menor mede 6, focos no eixo dos x e passa pelo ponto P - 2 5 ,2 .
Em cada um dos problemas 9 a 22, determinar a equação da elipse que satisfaz as condições dadas.13) centro C ( 0 ,0 ) , focos no eixo dos x , excentricidade e = 2 3 e passa pelo ponto 2 , - 5 3 .