Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 25.Exercício - Ex. 40
(a) Prove que a interseção de com qualquer plano que contém é reunião de duas retas concorrentes em .
(b) Prove que existem planos contendo e existem planos contendo cuja interseção com se reduz à origem.
Passo 1
Então pessoal, vamos começar olhando para aquele trecho ali “qualquer plano que contém ”.
Como é a “cara” de uma equação de um plano que contém ? Bom, é uma reta, certo? Uma reta que cruza a origem e vai na direção do eixo .
Uma forma de descrever essa reta é com essas duas equações planares:
Certo? Porque nós estamos na interseção desses dois planos.
Quando a gente sabe as equações planares de uma reta, dá pra encontrar a equação do feixe de planos que contêm essa reta.
Se as equações planares da reta são:
Então a equação do feixe é:
Então, no nosso caso:
Passo 2
Agora vamos substituir isso lá na equação da superfície :
Pela condição ali de cima:
E vamos chamar:
Para facilitar a vida. Substituindo isso:
E esse termo entre parênteses também é uma constante que a gente pode renomear:
Então:
Passo 3
Mas que lugar geométrico é esse? Vamos tirar a raiz quadrada dos dois lados:
Isso é o mesmo que:
E essa fórmula tem duas interpretações possíveis:
Essas equações descrevem dois planos como esses:
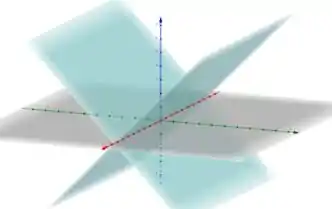
Quando esses planos intersectam uma superfície, o resultado são duas retas concorrentes, conforme esperado.
Passo 4
(b) Agora queremos mostrar que a interseção de com planos que intersectam e pode ser só a origem.
Para isso vamos lembrar da fórmula para o feixe de planos que contém uma reta. Se as equações planares da reta são:
Então a equação do feixe é:
A reta que intersecta tem como equações planares:
Afinal de contas, essa é a reta que contém a origem e está na direção do eixo (é o próprio eixo na verdade!).
E então a equação do feixe é:
A reta que intersecta tem como equações planares:
Então:
Passo 5
E agora vamos ver como isso se comporta quando a gente joga na fórmula da superfície :
Começando pelos planos que contém
Substituindo isso:
E essa equação tem solução sempre que esse coeficiente multiplicando o for positivo:
Como e são parâmetros livres, essa solução sempre vai existir, isso quer dizer que sempre existem planos que intersectam .
E tanto a equação dos planos quanto as de cruzam a origem:
Porque as duas equações aceitam a solução .
Passo 6
Quando pegamos o outro feixe de planos:
O argumento é totalmente análogo, é só trocar por :
Substituindo isso:
E a condição que sempre vai ter solução é:
Então sempre existe interseção, e as duas equações aceitam a origem como solução.
Resposta
Demonstração.