Enunciado
Álgebra Linear e Geometria Analítica - Reginaldo - Matrizes, Vetores e Geometria Analítica- Ed: 1º - Capítulo 1.1 - Ex. 1a
(a) AB − BA
Passo 1
Bom galera, esse exercício temos que ir por partes pra não nos perdermos nas contas. O enunciado nos deu os valores de A e de B. Ele está pedindo para fazermos AB - BA. Vamos começar fazendo AB, ou seja fazer a multiplicação de A * B.
Para fazermos a multiplicação de matrizes, devemos multiplicar as linhas da primeira matriz com as colunas da segunda matriz, ou seja, vamos pegar a primeira linha de A e multiplicar pela primeira coluna de B.
Vamos ter algo assim:
Simplificando vamos ter:
AB=
Passo 2
Agora nós precisamos achar o valor de BA. Vamos fazer a mesma coisa.
Precisamos multiplicar as linhas da primeira matriz pelas colunas da segunda matriz.
Vamos achar esse resultado:
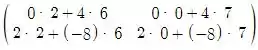
BA =
Simplificando temos:
BA =
Passo 3
Agora com os valores de AB e de BA, podemos fazer AB - BA
Para fazermos a subtração de matrizes, devemos subtrair os elementos nas posições equivalentes.
Vamos ter então:
AB - BA =
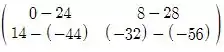
AB - BA =
Simplificando vamos ter que:
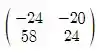
AB - BA =
Resposta
- AB - BA =