Enunciado
Álgebra Linear e Geometria Analítica - Reginaldo - Matrizes, Vetores e Geometria Analítica- Ed: 1º - Capítulo 1.1 - Ex. 3d
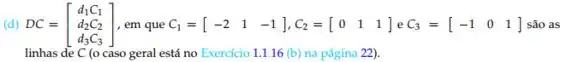
Passo 1
Bem pessoal esse exercício é bem parecido com o anterior. Vamos fazer primeiro a multiplicação das D e C.
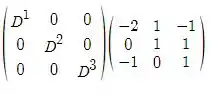
DC =
Fazendo a multiplicação de matrizes;
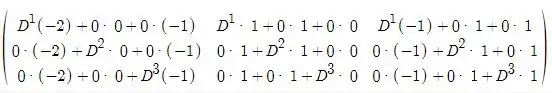
CD =
Simplificando vamos ter:
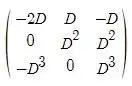
CD =
Passo 2
O enunciado nos disse que:
DC =
Sendo que ,, representa as linhas da matriz C
Passo 3
Vamos fazer uma comparação com o resultado de DC e ver se ele bate com o que o enunciado pede:
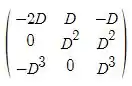
CD que encontramos =
Na primeira linha temos então:
= * - 2 = -2
= * 1 =
= * --1 = -
Assim fazemos para segunda e terceira linha.
Resposta
A afirmativa feita pelo enunciado está correta.
Exercícios de Livros Relacionados
Mostre que a matriz identidade I n é a única matriz tal que A I n = I n A = A para qualquer matriz A ,nxn . (Sugestão: Seja J n uma matriz tal que A J n = J n A = A . Mostre que J n = I n
Sejam A e B matrizes mxp e pxn , respectivamente. (b)Mostre que a i -ésima linha do produto A B é igual ao produto A i B , em que A i = a i 1 … a i p é a i -ésima linha de A , ou seja, se A = A 1 A 2
(a)Determine todas as matrizes A , 2 x 2 , que comutam com toda matriz B , 2 x 2 , ou seja, tais que A B = B A , para toda matriz B ,2 x 2 .
Se A é uma matriz tal que A^2 = 0 , então A = 0 ? Justifique.
Seja D = λ 1 0 … 0 0 λ 2 … 0 ⋮ ⋮ ⋱ ⋮ 0 … 0 λ n uma matriz diagonal nxn , isto é, os elementos que estão fora da diagonal são iguais a zero. Seja A = a 11 a 12 … a 1 n a 21 a 22 … a 2 n ⋮ ⋮ … ⋮ a n 1 a