Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 22.Exercício - Ex. 98

As retas s : y = x + 1 e t : y = 2 x + 1 / 2 são tangentes a uma parábola P , cuja diretriz é r : x = - 1 . Obtenha uma equação reduzida de P .

Passo 1

A equação de uma parábola com vértice na origem é dada por:

y 2 = 4 p x

E p = 1 , porém teremos que verificar se o foco dessa parábola está em que ponto do eixo x (pois a diretriz estando em x = a nos dá com certeza o foco no eixo x ) , até para saber se o vértice está na origem ou não.

A equação da reta tangente de uma parábola dado T = ( h , k ) como ponto de tangência é:

k y = 2 p x + 2 p h

k 2 = 4 h

Comparando a primeira equação com s nós teremos:

y = 2 k x + 2 h k

y = x + 1

Portanto:

2 k = 1 → k = 2

2 h k = 1 → h = 1

Logo nosso primeiro ponto de tangência está em ( 1,2 ) , o que se verifica se aplicarmos esse ponto na segunda equação.

Passo 2

E para y = 2 x + 1 2 :

2 k = 2 → k = 1

2 h k = 1 2 → h = 1 4

Então o segundo ponto de tangência será:

1 4 , 1

Passo 3

Agora vamos chamar o foco de F = ( a , b ) e descobrir as coordenadas desse foco ao fazer a distância desses pontos ao foco e a reta diretriz ser igual:

Para o ponto ( 1,2 ) temos:

1 + 1 = 1 - a 2 + 2 - b 2

4 = 1 - a 2 + 2 - b 2

Agora para o ponto 1 4 , 1 .

1 + 1 4 = 1 4 - a 2 + 1 - b 2

25 16 = 1 4 - a 2 + 1 - b 2

Esse sistema só dá certo para a = 1   e b = 0 , portanto o foco está em ( 1,0 ) e o vértice portanto está na origem. Logo a equação da parábola de fato é y 2 = 4 x . A figura das retas e da parábola pode ser vista abaixo.

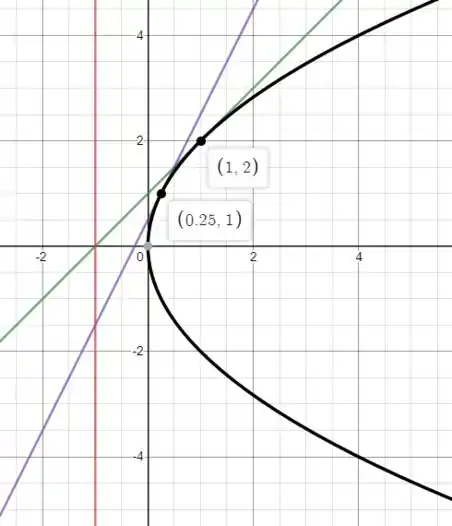
Onde y = x + 1 é a reta verde e y = 2 x + 1 2 a reta roxa, a reta diretriz é a vermelha.

Resposta

y 2 = 4 x

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em cada um dos Problemas de 27 a 36, determinar a equação reduzida, o vértice, o foco, uma equação da diretriz e uma equação do eixo da parábola de equação dada. Esboçar o gráfico.30. y 2 - 16 x + 2 y
Em cada um dos Problemas de 27 a 36, determinar a equação reduzida, o vértice, o foco, uma equação da diretriz e uma equação do eixo da parábola de equação dada. Esboçar o gráfico.28. x 2 - 2 x - 20 y
Em cada um dos Problemas de 27 a 36, determinar a equação reduzida, o vértice, o foco, uma equação da diretriz e uma equação do eixo da parábola de equação dada. Esboçar o gráfico.33. y = x 2 - 4 x +
Em cada um dos Problemas de 27 a 36, determinar a equação reduzida, o vértice, o foco, uma equação da diretriz e uma equação do eixo da parábola de equação dada. Esboçar o gráfico.36. 2 x 2 - 12 x - y
Em cada um dos Problemas de 27 a 36, determinar a equação reduzida, o vértice, o foco, uma equação da diretriz e uma equação do eixo da parábola de equação dada. Esboçar o gráfico.31. y = x 2 4 - 2 x