Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 22.Exercício - Ex. 97
A reta tangencia a parábola em um ponto de abscissa , e é a diretriz de . Obtenha uma equação reduzida da parábola.
Passo 1
As vezes a gente esquece mas a abcissa é o eixo horizontal, portanto o ponto de tangência é:
E como é a diretriz de , então sabemos que o foco está no eixo porém não podemos cravar onde, só podemos dizer que a distância desse ponto de tangente até a diretriz é igual então:
E a melhor forma de escrever essa equação é com posição do foco em , pois aí de maneira fácil com a diretriz em nós conseguimos dizer que o parâmetro vale e vértice na origem, nos dando uma equação de parábola igual a:
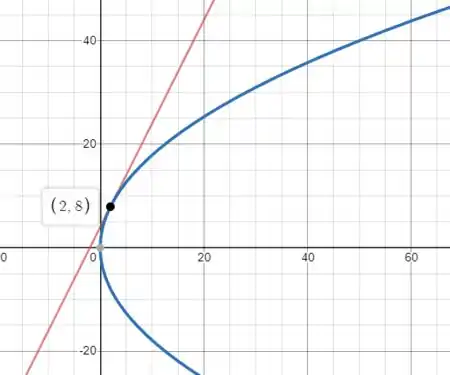
A imagem dessa parábola pode ser vista abaixo.
Passo 2
Utilizando a coisa não daria muito certo pois, teríamos que o meio entre e é portanto o vértice dessa parábola estaria em , e o parâmetro cairia para , Portanto a equação seria:
A reta até bate com , só que essa reta forma uma secante com a parábola.