Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 22.Exercício - Ex. 117
São dados, graficamente, o eixo transverso e os focos e ) de uma hipérbole. Descreva um método de construção com régua e compasso:
- de pontos da hipérbole, baseado apenas na Definição 22-9;
- da reta tangente e da reta normal à hipérbole, conhecido o ponto de tangência .
Passo 1
A definição 22-9, nos diz que:
Dado dois pontos e distanciados de , a hipérbole é o conjunto de pontos de um plano tal que , onde .
- Baseado na definição acima, podemos pensar no seguinte procedimento:
- Desenhamos o eixo e os focos , respeitando as condições de existência da elipse;
- Tomemos um ponto fora do segmento ;
- Traçamos a circunferência de centro e raio ;
- Traçamos a circunferência de centro e raio ;
- As intersecções das circunferências nos darão dois pontos da hipérbole.
Veja o roteiro acima esquematizado na figura abaixo.
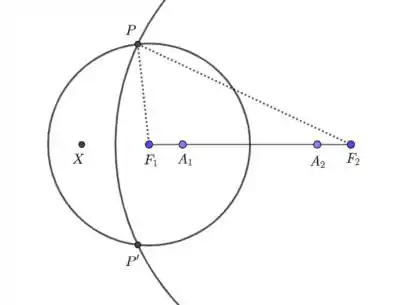
Note que seguindo o roteiro acima, sempre iremos garantir que
pois é o raio da primeira circunferência, que vale ; é raio da segunda circunferência que vale . Logo, .
Passo 2
Pela propriedade da reflexão, a reta tangente contém a bissetriz de . Portanto, basta desenhar tal bissetriz! A reta normal será perpendicular à reta tangente no ponto .
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Em cada um dos problemas 1 a 10, determinar o centro, os vértices, os focos e a excentricidade das hipérboles dadas. Esboçar o gráfico x 2 - 2 y 2 - 8 = 0
Em cada um dos problemas 1 a 10, determinar o centro, os vértices, os focos e a excentricidade das hipérboles dadas. Esboçar o gráfico y 2 - 4 x 2 = 1
Em cada um dos problemas 1 a 10, determinar o centro, os vértices, os focos e a excentricidade das hipérboles dadas. Esboçar o gráfico 3 x 2 - y 2 + 3 = 0
Em cada um dos problemas 1 a 10, determinar o centro, os vértices, os focos e a excentricidade das hipérboles dadas. Esboçar o gráfico 4 x 2 - 5 y 2 + 20 = 0
Em cada um dos problemas 1 a 10, determinar o centro, os vértices, os focos e a excentricidade das hipérboles dadas. Esboçar o gráfico 2 y 2 - 4 x 2 = 1