Enunciado
Álgebra Linear e Geometria Analítica - Reginaldo - Matrizes, Vetores e Geometria Analítica- Ed: 1º - Capítulo 7.3 - Ex. 10
Seja S o conjunto dos pontos do espaço que satisfazem a equação
com a, b, c, d, e, f, g, h, i, j ∈ R, sendo a, b, c, d, e, f não simultaneamente nulos. Sejam a’, b’ e c’ raízes de
Mostre que:
a) Se a’, b’ e c’ tiverem mesmo sinal, então S e um elipsoide, um ponto ou o conjunto vazio;
b) Se a’, b’ e c’ forem não nulos e não tiverem mesmo sinal, então S e uma hiperboloide de uma folha, de duas folhas, ou um cone elíptico;
c) Se apenas um entre a’, b’ e c’ for nulo, então S e um paraboloide elíptico, hiperbólico, um cilindro ´ elíptico, hiperbólico, dois planos concorrentes, uma reta ou o conjunto vazio;
d) Se exatamente dois entre a’, b’ e c’ forem nulos, então S e um cilindro parabólico, um par de planos paralelos ou um plano.
Passo 1
Fala aí pessoal tudo blz?
Nessa questão sabendo que,
com a, b, c, d, e, f, g, h, i, j ∈ R, sendo a, b, c, d, e, f não simultaneamente nulos. Sejam a’, b’ e c’ raízes de
Mostre que:
a) Se a’, b’ e c’ tiverem mesmo sinal, então S e um elipsoide, um ponto ou o conjunto vazio;
b) Se a’, b’ e c’ forem não nulos e não tiverem mesmo sinal, então S e uma hiperboloide de uma folha, de duas folhas, ou um cone elíptico;
c) Se apenas um entre a’, b’ e c’ for nulo, então S e um paraboloide elíptico, hiperbólico, um cilindro elíptico, hiperbólico, dois planos concorrentes, uma reta ou o conjunto vazio;
d) Se exatamente dois entre a’, b’ e c’ forem nulos, então S e um cilindro parabólico, um par de planos paralelos ou um plano.
Só vem e confia que juntos vamos resolver esta questão
Passo 2
Na letra (a) sabendo que a’, b’ e c’ tiverem mesmo sinal, com S sendo um elipsoide para determinarmos um ponto ou conjunto vazio temos que,
Para o elipsoide valendo,
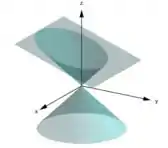
Já na letra (b) para a’, b’ e c’ forem não nulos e não tiverem mesmo sinal, então S e uma hiperboloide de uma folha, de duas folhas, ou um cone elíptico,
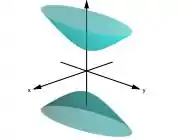
Na letra ( c ) sendo apenas um entre a’, b’ e c’ for nulo, então S e um paraboloide elíptico, hiperbólico, um cilindro elíptico, hiperbólico, dois planos concorrentes, uma reta ou o conjunto vazio;
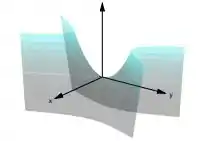
E por fim na letra (d) temos que se exatamente dois entre a’, b’ e c’ forem nulos, então S e um cilindro parabólico, um par de planos paralelos ou um plano;
Espero ter ajudado, bons estudos e até a próxima.
Resposta
a)
b)
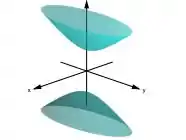
c)
d)