Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 25.Exercício - Ex. 28
Prove que é um paraboloide elíptico e faça um esboço.
Passo 1
Bom, vamos começar lembrando qual é a definição de um paraboloide elíptico. É qualquer superfície que tenha essa equação reduzida aqui:
Onde e são número reais positivos, e são um sistema de coordenadas ortogonais.
Vamos dar uma olhada na equação do enunciado:
Logo de cara aparece um problema: aparecem multiplicando um ao outro! Precisamos dar um jeito nisso.
A melhor forma de resolver esse tipo de problema é aplicando uma mudança de coordenadas.
Quando queremos nos livrar de termos do tipo , ou , é melhor usar uma translação de coordenadas.
Quando queremos nos livrar de termos do tipo , é melhor usar uma rotação de coordenadas.
Passo 2
Como o nosso problema só está nas variáveis e , vamos fazer uma rotação no plano , ou seja, em torno do eixo :
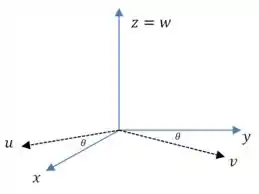
E vamos lembrar da matriz de rotação, que é uma forma fácil de lembrar como fica essa rotação.
No nosso caso, e são o resultado de uma rotação de e por um ângulo no sentido anti-horário:
Essa matriz faz justamente isso: rotacional as coordenadas por um ângulo no sentido anti-horário.
Multiplicando aquelas matrizes, encontramos o seguinte:
Beleza, agora vamos substituir essas expressões de e na equação lá de cima:
Passo 3
Voltando na nossa equação:
E substituindo:
Agora vamos abrir esses produtos notáveis. Um de cada vez para evitar confusão:
Somando o primeiro e o terceiro termos, vamos simplificar bastante as contas:
Os dois termos com se cancelam, e podemos colocar os outros em evidência:
E lembrando que :
E agora, para voltar na fórmula de , ficamos com:
Usando a expressão que a gente encontrou para o segundo termo:
E agora temos que lembrar de outras duas identidades importantes:
Então:
Beleza, agora queremos nos livrar daquele termo com . A única forma de fazer isso é forçando isso aqui:
E como , vamos usar:
Nesse caso:
E , ficamos com:
Ah, e também vamos fazer :
Passo 4
Beleza, agora vamos voltar à equação do paraboloide:
E como e também são coordenadas ortogonais, podemos escrever essa fórmula como:
Dá pra escrever a nossa equação nessa forma? Vamos tentar:
Já está nessa forma! É só fazer e :
Pronto, provamos que dá um paraboloide elíptico!
Passo 5
Para fazer um esboço da superfície, vamos considerar o que acontece quando é uma constante:
A equação do paraboloide elíptico é:
Que dá uma elipse em um plano paralelo a ao plano :
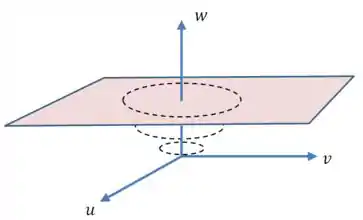
Agora é só “juntar” todas essas curvas para encontrar um esboço como esse:
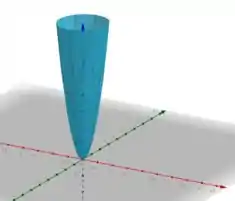
Resposta
Demonstração. Temos que fazer uma rotação de em torno do eixo para obter a equação do paraboloide na forma reduzida.