Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 25.Exercício - Ex. 38c
Identifique a quádrica descrita pela equação dada.
(c)
Passo 1
Bom, vamos dar uma olhada nessa equação:
O nosso problema aqui é encontrar a equação reduzida.
Logo de cara aparece um problema: aparecem multiplicando um ao outro! Precisamos dar um jeito nisso.
A melhor forma de resolver esse tipo de problema é aplicando uma mudança de coordenadas.
Quando queremos nos livrar de termos do tipo , é melhor usar uma rotação de coordenadas.
Passo 2
Como o nosso problema só está nas variáveis e , vamos fazer uma rotação no plano , ou seja, em torno do eixo :
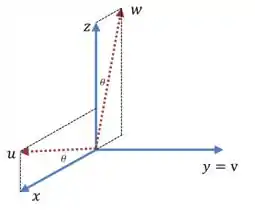
E vamos lembrar da matriz de rotação, que é uma forma fácil de lembrar como fica essa rotação.
No nosso caso, e são o resultado de uma rotação de e por um ângulo no sentido anti-horário:
Essa matriz faz justamente isso: rotacionar as coordenadas por um ângulo no sentido anti-horário.
Multiplicando aquelas matrizes, encontramos o seguinte:
Beleza, agora vamos substituir essas expressões de e na equação lá de cima:
Passo 3
Voltando na nossa equação:
Para simplificar, vamos começar olhando só para esses dois primeiros termos:
Porque é neles que pode aperecer o produto que está dando trabalho.
E vamos substituir com as expressões ali de cima:
E o termo misturando que causou problemas é:
Isso tudo também ia ficar muito confuso se a gente somar as três expressões. Então primeiro vamos ver quais termos sobram com o produto .
Nessas simplificações aí de cima, nós usamos essas identidades aqui:
Como a nossa expressão era:
Então, substituindo, esse termo aqui vai aparecer:
Então, se a gente quer eliminar esse único termo em que aparece o produto , temos que fazer:
E a solução mais simples para isso é:
Passo 4
Beleza, agora vamos voltar lá nas expressões para , e :
Aplicando de novo aquelas identidades, mas dessa vez considerando todos os termos:
Ficamos com:
Substituindo , e lembrando que:
Então:
E agora substituímos na expressão que aparece na equação do enunciado:
E usando essa identidade trigonométrico aqui:
Ficamos com:
Ok, já foi uma simplificação bem grande!
Passo 5
Agora vamos voltar na equação original:
A gente já viu que esses últimos três termos viram:
Então:
Agora vamos substituir e com as mesmas fórmulas de antes:
A equação vira:
E quando a gente colocar , e lembrar que:
Didivindo tudo por :
Passo 6
A finalmente, vamos ao que interessa, qual é a superfície quádrica descrita por essa equação?
Como só temos duas variáveis, sabemos que é uma equação quádrica cilíndrica. E como as duas variáveis estão ao quadrado, podemos ter:
Que daria uma cilíndrica elíptica, ou:
Que dá uma cilíndrica hiperbólica. Como na nossa equação as duas variáveis tem os sinais trocados (uma positiva e uma negativa):
Ela só pode ser uma cilíndrica hiperbólica. Pronto, pode parar por aqui, já sabemos qual é a superfície.
Mas... Se você quiser deixar na forma reduzida ali de cima, é só completar os quadrados para encontrar essa igualdade aqui:
Então:
Que é praticamente igual à forma reduzida! A única diferença é que a coordenada está deslocada por uma distância de .
Para corrigir isso você pode fazer uma translação de coordenadas (assim como fizemos uma rotação lá em cima):
Então:
Pronto! Agora estamos na forma reduzida. E mais uma vez confirmamos que a superfície é uma quádrica cilíndrica hiperbólica.
Resposta
A equação é uma quádrica cilíndrica hiperbólica.