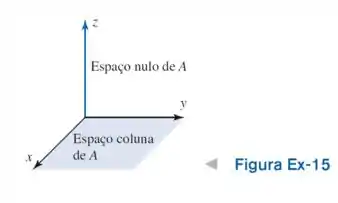
(a) Seja A = 010100000 Mostre que, em relação a um sistema de coordenadas retangulares x y z no espaço tridimensional, o espaço nulo de A consiste em todos os pontos no eixo z , e que o espaço coluna consiste em todos os pontos no plano x y (ver figura).(b) Encontre uma matriz 3 × 3 cujo espaço nulo seja o eixo x e cujo espaço coluna seja o plano y z .

Enunciado

Fala aê!! Tudo certo? Vamos resolver essa questão?!

(a) Para este item, colocaremos, inicialmente, a matriz na sua forma escalonada. Ficando:

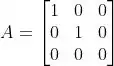
O espaço nulo de uma matriz consiste no conjunto de vetores que satisfação .

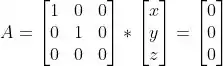
logo temos que:

Assim, a solução geral do sistema é portanto, o espaço nulo de é o eixo .

O espaço coluna tem que ser uma combinação linear dos vetores colunas da matriz logo:

Que é uma combinação linear de e , ou seja, o plano

(b) De modo semelhante ao item (a), podemos observar a seguinte matriz

Calculando o espaço nulo dela temos:

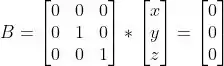
resolvendo as equações temos que:

Nela, temos que é

Portanto, o espaço nulo de é o eixo

Calculando o espaço coluna de temos:

Que é uma combinação linear de e , ou seja, o plano .

Veja a resolução.