Enunciado
Álgebra Linear e Geometria Analítica - Anton - Álgebra Linear- Ed: 10º - Capítulo 4.6 - Ex. 19
Sejam a base canônica de e a base que resulta quando os vetores de são refletidos em torno da reta que faz um ângulo com o eixo positivo.
a) Encontre a matriz de transição .
b) Seja e mostre que .
Passo 1
Fala pessoal, nesse problema vamos falar um pouco sobre a reflexão de pontos no plano cartesiano.
O enunciado forneceu a base canônica com
Para achar os vetores de , temos que refletir os vetores e em torno da reta . Essa é reta que faz um ângulo com o eixo positivo.
Vamos ver o que acontece com quando é refletido:
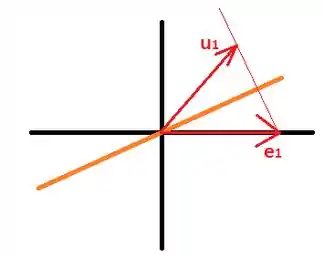
Quando refletimos , obtemos cuja norma deve ser . Além disso, o ângulo que faz com o eixo é . Portanto, as coordenadas de são
Analagamente, refletindo em torno dessa reta, obtemos que que forma um ângulo com o eixo . Portanto, o ângulo formado com o eixo é
Assim,
Ou ainda,
Note que
Para construir a matriz de mudança de base de para , pegamos as coordenadas dos vetores de escritos na base e as colocamos nas colunas da matriz:
Passo 2
A matriz achada no item (a) é chamada de :
Sabemos que é a inversa de . Para achar a inversa, usamos o truque das matrizes :
Assim,
Como , temos que
Mas note também que a transposta de é
Portanto,