Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios de Matriz de Mudança de Base - Lista de Exercícios Resolvida

Ver Teoria

Questão 1

Sejam α ,   β ,   γ bases do espaço vetorial V , e sejam

A = I α ← β ,   B = I γ ← β ,   C = I γ ← α

matrizes de mudança de base. Então:

a   B - 1 C = A

b   B C - 1 = A - 1

c   B C - 1 = A

d   B - 1 C = A - 1

Ver solução completa

Questão 2

Seja P 1 o espaço euclidiano dos polinômios p x = a x + b e considere a base β = 2 x - 2,2 x + 2 . Se γ é uma base tal que a matriz de mudança de base de β para γ

I γ ← β = 1 - 2 1 - 1

então a base γ é:

a   γ = - 4 x , 6 x - 2

b   γ = - 4 x - 6 , - 2

c   γ = { 2 x - 2 ,   2 x + 2 }

d   γ = { 8 ,   8 x }

Ver solução completa

Questão 3

À questão “Seja L : R 2 ⟶ R 2 a transformação linear definida por L 1,0 = ( 1,0 ) e L 1,1 = ( 0 , 0 ) . Encontre a matriz de L associada a base canônica de R 2 ”, Joãozinho respondeu:

A resposta do Joãozinho está errada pois L 1,1 deveria dar ( 0,0 ) . Indique qual foi o erro que Joãozinho cometeu e explique a sua afirmação.

OBS: Este item não pede a resposta certa, pede para explicar ao Joãozinho o seu erro.

Ver solução completa

Questão 4

Em ℘ 2 , considere a base β = { 1 + X ,   X ,   1 - X 2 } . Seja α uma outra base tal que I β α = 1 1 1 1 2 1 0 1 1 .

a) Determine o polinômio p X ∈   ℘ 2 tal que p X α = 1 ,   - 1 ,   2 T .

b) Determine a matriz I α β .

Ver solução completa

Questão 5

À questão “Seja L : R 2 ⟶ R 2 a transformação linear definida por L 1,0 = ( 1,0 ) e L 1,1 = ( 0 , 0 ) . Encontre a matriz de L associada a base canônica de R 2 ”, Joãozinho respondeu:

( c ) A resposta do Joãozinho está errada pois L 1,1 deveria dar ( 0,0 ) . Indique qual foi o erro que Joãozinho cometeu e explique a sua afirmação.

OBS: Este item não pede a resposta certa, pede para explicar ao Joãozinho o seu erro.

Ver solução completa

Questão 6

Considere a transformação linear T : R 2 ⟶ R 2 definida pela figura abaixo:

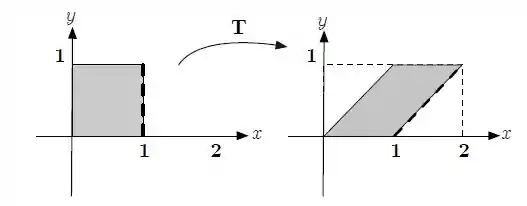
( a ) Determine uma expressão para a imagem T ( x , y ) de um vetor x , y ∈ R 2

( b ) Determine T β ← γ onde β = 1,0 , 0,1 e γ = 1,1 , 1 , - 1

( c ) Determine as matrizes de mudança de base de β para γ e de γ para β .

Ver solução completa

Questão 7

Sejam α , β , γ bases do espaço vetorial V , e sejam

A = I α ← β                     B = I γ ← β                     C = I γ ← α

matrizes de mudança de base. Então:

a   B - 1 C = A

b   B C - 1 = A

c   B C - 1 = A - 1

d   B - 1 C = A - 1

Ver solução completa

Questão 8

Considere os vetores u 1 ,   u 2 e u 3   de R 3 cujas coordenadas na base canônica ε = i ,   j ,   k de R 3   são:

u 1 ε = 1 ,   2 ,   1 ,     u 2 ε = a ,   0 ,   1 ,     u 3 ε = 0 ,   b ,   c ,  

Onde a ,   b ,   c são números reais todos diferentes de 0 .

  1. Determine valores de a ,   b ,   c para que os vetores u 1 ,   u 2 ,   u 3 sejam linearmente dependentes e o subespaço gerado por eles seja o plano vetorial:

    2. π = v ∈ R 3 : v ε = x ,   y ,   z ,     o n d e   2 x + y - 4 z = 0

  2. Suponha agora que

    3. β = u 1 , u 2 ,   u 3

    É uma base de R 3 e que u é um vetor de R 3 cujas coordenadas na base β e canônica ε são:

    u ε = 3 ,   4 ,   3 ,     u β = 1 ,   1 ,   1

    Determine os valores de a ,   b ,   c .

  3. Seja α = v 1 ,   v 2 ,   v 3 uma base de R 3 . Considere a nova base de R 3 :

    4. δ = v 1 + v 3 ,   v 1 + v 2 ,   v 2 + v 3

    Sabendo que as coordenadas do vetor w na base α são:

    w α = 1 ,   1 ,   1

    Determine as coordenadas de w δ de w na base δ .

  4. Considere o plano ρ de equação cartesiana:

ρ = v ∈ R 3 : v ε = x ,   y ,   z ,     o n d e     x - 2 y + z = 0

E sua base:

γ = w 1 ,   w 2

Onde

w 1 ε = 1 ,   0 ,   - 1 ,     w 2 ε = 1 ,   1 ,   1  

Considere o vetor m de ρ cujas coordenadas na base canônica são

m ε = 2 ,   3 ,   4

Determina as coordenadas de m na base γ .

Ver solução completa

Questão 9

Considere a transformação linear T : R 3 → R 3   cuja matriz na base canônica a do R 3 é

T a a = 3 0 0 0 2 1 0 1 2

  1. Encontre uma base ortonormal β (referente ao produto interno canônico) tal que T β β é diagonal.
  2. Escreva T β β .
  3. Escreva T a β

Ver solução completa

Questão 10

Seja T : R 2 → P 1 R uma transformação linear. Considere α = 1,1 , - 1,0 e β = - x , 2 + x bases para R 2 e P 1 R respectivamente. Temos que T β α = 1 2 3 0 .

b Considere a base δ = 1 , x de P 1 R e determine T δ α .

Ver solução completa

Questão 11

Seja V = P 2 o espaço vetorial dos polinômios de grau até 2 , e sejam os subespaços W 1 = 1 + x , 1 - x , W 2 = x 2 .

a Qual as dimensões de V , W 1 e W 2 ? Justifique!

b Defina W 1 ∩ W 2 , W 1 ∪ W 2 e W 1 + W 2 , determine quais são subespaços de V e obtenha bases para esses subespaços.

c Justifique porque W 1 + W 2 = V , e ache a matriz de mudança de base entre α , a base canônica de V , e β , a base obtida acima (item b ).

d Se v → β = 1 1 1 , ache v → α .

Ver solução completa

Questão 12

Considere as bases do R 2

γ = - 1,1 , - 1,0

σ = 0,1 , - 1 , - 1

E a transformação linear T : R 2 → R 2 cuja matriz na base γ é:

T γ = 3 - 2 1 - 1

(a) Determine explicitamente as matrizes de mudança de base da base γ   para a base σ e da base σ para a base γ .

(b) Determine explicitamente a matriz T σ da transformação linear T na base σ .

Ver solução completa

Questão 13

Seja P 1 o espaço dos polinômios p x = a x + b e considere a base β = 2 x - 2,2 x + 2 . Se γ é uma base tal que a matriz de mudança de base de β para γ é I γ ← β = 2 - 3 1 - 1 , então a base γ é:

a   γ = 8,8 x

b   γ = - 4 x - 10 , - 2

c   γ = - 4 x , 10 x - 2

d   γ = 2 x - 2,2 x + 2

Ver solução completa

Questão 14

Sejam u = ( 1 , - 1 ) , v = ( 1,2 ) e γ = { u , v } . Considere T   : R 2 → R ² uma transformação linear tal que

T γ = 1 2 - 1 3

  1. Seja w = - 3 u + 2 v . Determine:

a.1) [ T w ] γ

a.2) T ( w )

b) Determine T ( 1,0 ) e T ( 0,1 ) .

c) Determine [ T ] ε , onde ε é a base canônica de R ² .

Ver solução completa

Questão 15

Responda:

Seja T : P 1 ⟶ P 2 uma transformação linear tal que T a + b t = a + a t + b t 2   e seja α = t + 1 , t - 1 uma base de P 1 e β = t 2 + 1 ,   t - 1 , t + 1 uma base de P 2 .   Determine T β α .

Ver solução completa

Questão 16

Decida se cada afirmação abaixo é verdadeira ou falsa. Se a afirmação for verdadeira, apresente uma demonstração. Se a afirmação for falsa, exiba explicitamente um contraexemplo.

(b.1) Se A   = 1 - 1 3 1 , então A - 1 = 1 4 1 1 - 3 1

(b.2) Se T :   R 2 → R 2     é uma transformação linear tal que sua matriz na base β = 1 ,   3 , - 1 ,   1 é T β = 2 1 0 - 1 ,     então T ( x ,   y )   =   ( - x   + y ,   2   y ) .

Ver solução completa

Questão 17

Seja W = a b 0 c ;   ∀ a , b , c ∈ R subespaço de M 2 × 2 R .   Seja β uma base de   W :   β = 1 0 0 0 , 1 1 0 0 , 1 1 0 1 . Encontre a base α de W   tal que I β α = 1 2 0 0 1 - 1 2 0 1 .

Ver solução completa

Questão 18

Considere a base γ = 1 0 0 0 ,   0 1 0 0 ,   0 - 1 1 0 ,   0 0 0 - 1 e a matriz de mudança de base

I γ α = 1 2 1 1 2 - 1 2 0 - 1 1 0 0 0 1 1 1

a) Determine as matrizes de base α .

b) Se V α = 3 - 1 1 2 , determine V γ .

Ver solução completa

Questão 19

Seja T :   R 3 → R 3 a transformação linear dada por T x 1 ,   x 2 ,   x 3 = ( x 1 - x 2 + x 3 ,   x 1 - 2 x 3 ,   2 x 1 + x 2 ) .

a) Sendo C a base canônica de R 3 , determine T C C .

b) Com respeito à base B = { 1 ,   0 ,   - 1 ,   - 1 ,   0 ,   2 ,   0 ,   2 ,   0 } , determine I B C e T B C .

c) Seja agora S :   R 2 → R 2 a transformação linear tal que S 1 ,   1 = ( 1 ,   2 ) e S - 2 ,   0 = ( 3 ,   4 ) . Determine S ( x ,   y ) .

Ver solução completa

Questão 20

Seja T : P 1 → P 1 uma transformação linear. E sejam α = 1 + x , 1 - x e β = 2 , - x bases do P 1 . Considere T β α = 1 2 2 2

b Sendo a transformação inversa T - 1 : P 1 → P 1 , determine T - 1 α β .

Ver solução completa

Questão 21

Seja β = 1 + x , x , x 2 + x uma base para P 2 = a 0 + a 1 x + a 2 x 2 ; ∀ a i ∈ R , i = 0,1 , 2 . E seja α outra base para o espaço vetorial P 2 tal que I β α = 1 0 1 0 2 1 2 0 - 1 .

a Determine o vetor v tal que v α = 2 1 0 .

b Encontre a base α .

c Calcule a matriz I α β .

Ver solução completa

Questão 22

Sejam B e C duas bases de V 3 , e u → ∈ V 3 . Se u → = - 1,1 , - 1 B e :

M B , C = 1 - 2 1 2 - 3 - 1 - 1 1 3

A matriz de mudança de base, então temos:

  1. u → = 10,6 , 1 C ;
  2. u → = - 4 , - 4 , - 1 C ;
  3. u → = - 3 ,   - 4 ,   - 1 C ;
  4. u → = - 4 ,   - 6 ,   - 1 C ;
  5. u → = 20,6 , 1 C ;

Ver solução completa

Questão 23

Dizemos que duas matrizes A , B ∈ M 2 × 2 ( R ) comutam se satisfazem A B = B A . Considere o conjunto C ( A ) de todas as matrizes que comutam com A

C A = B ∈ M 2 × 2 R A B = B A }

( b ) Seja Q uma matriz inversível e A ' = Q - 1 A Q . Mostre que a transformação linear S definida por S B = Q - 1 B Q é uma bijeção de C ( A ) para C ( A ' ) .

(Dica: Verifique o contra-dominio de S e exiba a transformação inversa S - 1 .)

Ver solução completa

Questão 24

Considere as bases de vetores ε = { i , j , k } e β = v 1 , v 2 , v 3 de R 3 onde

i = 1,0 , 0 ,   j = 0,1 , 0 ,   k 0,0 , 1

v 1 = i = 1,0 , 0 ,   v 2 = i + j = 1,1 , 0 ,   v 3 = i + j + k = ( 1,1 , 1 )

Considere a transformação linear T : R 3 → R 3 definida por

T i = 0 = 0,0 , 0 ,   T j = i ,   T k = 2 j

Determine:

(a) A matriz T ε   de T na base ε .

(b) As matrizes de mudança de base da base ε para a base β e da base β para a base ε .

(c) A matriz T β de T   na base β .

Considere agora o espaço vetorial P 2 dos polinômios de grau menor ou igual a 2 e suas bases

γ = p i x = 1 , p j x = x , p k x = x 2

η = q 1 x = p i x , q 2 x = p i x + p j x ,   q 3 x = p i x + p j x + p k x

Podemos também usar a notação:

γ = 1 , x , x 2

η = 1,1 + x , 1 + x + x 2

Considere a transformação linear D : P 2 → P 2 que corresponde à derivada, definida por:

D p i x = D 1 = 0 ,   D p j x = D x = 1 , D p k x = D x 2 = 2 x

(d) Determine as matrizes D γ de D na base γ e D η de D   na base η .

Ver solução completa

Questão 25

Seja β = 2,2 , - 4,6 . A matriz que, ao multiplicar um vetor qualquer x , resulta nas coordenadas de x com relação à base β é

a   2 - 4 2 6

b   2 - 4 2 6 - 1

c   2 2 - 4 6

d   2 2 - 4 6 - 1

Ver solução completa

Questão 26

Sejam α = { 1,1 , - 1,1 } e β = { 1,6 , 1,7 } duas bases de R 2 . A matriz I β ← α   de mudança de base de α para β é igual a:

(a) 13 - 2 1 0

(b)   6 - 8 - 5 7

(c) 6 - 5 - 8 7

(d)   13 1 - 2 0

Ver solução completa

Questão 27

Sejam

Β = { e → 1 ,   e → 2 , e → 3 } e C = { f → 1 , f → 2 , f → 3 }

Bases de V 3 e considere o vetor v → = 2 ,   - 1 ,   3 Β . Denote por M β C a matriz cujas colunas são [ f → 1 ] β , f → 2 β ,   f → 3 β .   Se

M β C = 1 - 1 1 2 - 3 1 - 1 1 - 2

Então as coordenadas de v → na base C serão:

a) 6 ,   10 ,   - 9 ;

b) ( 17 ,   10 ,   - 5 ) ;

c) 4 ,   10 ,   - 9 ;

d) 6,4 ,   - 9 ;

e) ( 15 ,   10 ,   - 5 ) ;

Ver solução completa

Questão 28

Sejam α = 1,0 , 0,1 e β = 5,3 , 7,4 duas bases de R 2 . A matriz de mudança da base α para a base β é igual a

( a ) 5 7 3 4

( b ) - 4 7 3 - 5

c - 4 3 7 - 5

( d ) 5 3 7 4

Ver solução completa

Questão 29

Sejam E e F bases de V 3 . Suponha que E = e 1 , e 2 , e 3 e que

e 1 = x , y , z F

e 2 = 0,3 , 3 F

e 3 = 0,0 , 2 F

Seja M ∈ M 3 ( R ) a matriz que satisfaz M u F = u E , para todo u ∈ V 3 . Considere o vetor v ∈ V 3 tal que v = 1,1 , 1 E . Sabendo que v = 2,1 , 3 F , é correto afirmar que o determinante de M é igual a

a) 12

b) 24

c) 3

d) 1 3

e) 1 12

f) 1 24

Ver solução completa

Questão 30

Seja α = 1 , 0,1 , 0,1 , 1 , - 1,0 , 0 e β = v 1 , v 2 , v 3 bases do espaço vetorial R 3 . Seja I β α = 2 1 0 3 1 1 0 3 2

a Determine para o vetor v = 1 , 2,3 suas coordenadas em β : v β

b Para δ = 0 , - 1,0 , 1,0 , 0 , 0,0 , 1 calcule a matriz I γ α

Ver solução completa

Questão 31

Denote por B a base de R 2 dada por

B = { 1,0 ,   ( 2 ,   1 ) }

E por C a base canônica de R 2 . Seja T : R 2 → R 2 a transformação linear tal que:

T B C = 2 - 1 2 1

Temos que a soma das entradas na diagonal principal da matriz T ∘ T C é igual a:

Escolha uma opção:

  1. 4
  2. 3
  3. - 7
  4. - 1
  5. 1 / 2

Ver solução completa

Questão 32

Sejam α = 1,1 , - 1,1 e β = 1 , - 4 , - 3,13 duas bases de R 2 . A matriz I β ← α de mudança de base de α para β é igual a:

a   9 2 17 4

b   16 5 - 10 - 3

c   16 - 10 5 - 3

d   9 17 2 4

Ver solução completa

Questão 33

Considere as bases B e C de P 2 ( R ) dadas por:

B = { 1 + t + t 2 ,   1 - 7 t + t 2 ,   t + t 2 } e C = { 7 + 2 t ,   3 + t ,   t 2 }

Denotando por I :   P 2 R → P 2 ( R ) a transformação identidade, teremos que a soma dos elementos na diagonal principal da matriz I B C será igual a:

  1. - 52
  2. 52
  3. 65 / 8
  4. 63 / 8
  5. 6

Ver solução completa

Questão 34

Em P 2 considere a base β = 1 + x , x 2 , 1 - x e seja

I β α = - 1 1 0 0 - 1 1 2 1 2

a Encontre p x tal que p x α = 3 4 0

b Encontre a base α de P 2 .

Ver solução completa

Questão 35

Considere as seguintes bases para R 2 :

α = 1,0 , 0,1 e β = 1,1 , 1,2 . Dado que o vetor de coordenadas de v → na base α é a , b T , qual é o vetor de coordenadas de v → na base β ?

a   2 a - b , b - a T

b   3 a - b , 2 b - a T

c   2 b - a , 3 a - b T

d   b - a , 2 a - b T

Ver solução completa

Questão 36

Seja T : R 2 → R 2 uma transformação linear e α , β e γ bases do R 2 tais que

e

(a) Sabendo que v β = - 1 3 , determine v γ .

(b) Sabendo que α = { 1,2 , 0 , - 1 } , determine T v .

Ver solução completa

Questão 37

Seja T : P 1 ( R ) → P 1 ( R ) uma transformação linear, sejam α = { x , 1 - x } e β = { 2 - x ,   1 + 2 x } bases de P 1 R , e [ T ] α α = 1 2 3 4 .

  1. Para v = 3 + 2 x   calcule sua imagem T v .
  2. Determine a matriz mudança de base [ I ] α β .
  3. Determine a matriz da transformação [ T ] β β .

Ver solução completa

Questão 38

Considere, em E 3 , o cubo de vértices A , B , C , D , E , F , G , H e aresta unitária, conforme a figura

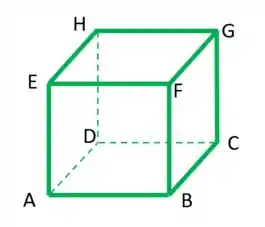
Suponha V 3 orientado de modo que a base B = A B , A C , A E seja positiva, e considere os vetores u = 2 , - 2,1 B e v = - 1,2 , 1 B . Então, as coordenadas, em relação à base B , do produto vetorial u ∧ v são

a) - 4,1 , 1

b) - 5,1 , 2

c) - 5 , - 3,1

d) - 3 , - 2,1

e) - 3 , - 1 , - 1

f) - 4 , - 3,2

g) - 7,2 , 1

h) - 5,2 , - 1

Ver solução completa

Questão 39

Considere o espaço vetorial R 2 munido do seu produto interno usual. Sejam T : R 2 → R 2 e S : R 2 → R 2 os operadores lineares tais que:

T B C = 5 - 5 / 2 0 5 / 2                   e                       S C B = 2 0 - 1 - 1

Em que B e C são as bases de R 2 dadas por:

B = 2,1 , 1 , - 2               e                 C = { 1,1 , ( 1 , - 1 ) }

Assinale a alternativa correta:

  1. T é simétrico e S não é simétrico;
  2. T e S são ambos simétricos;
  3. Nem T nem S são simétricos e as matrizes T B e S B são semelhantes;
  4. Nem T nem S são simétricos e as matrizes T B e S B não são semelhantes;
  5. S é simétrico e T não é simétrico.

Ver solução completa

Questão 40

Considere a base

B = { 1 , t + 1 ,   t 2 + t + 1 }

De P 2 ( R ) , a base

C = { 1,0 , 1 ,   1,1 , 0 , ( 0,1 , 1 ) }

De R 3 e a base D = { 1 , t , t 2 } de P 2 ( R ) . Sejam

T : P 2 R → P 2 R                         S : P 2 R → R 3

Transformações lineares tais que:

S 1 = 2,2 , 2 ,                     S t + 1 = 3,5 , 2 ,                   S t 2 + t + 1 = ( 2,1 , 1 )

E:

S ∘ T B C = 6 5 3 12 5 0 4 0 - 1

Temos que o determinante da matriz T D é igual a:

  1. 10
  2. - 30
  3. - 10
  4. 30
  5. - 3

Ver solução completa

Listas de Exercícios Resolvidos

Lista de Introdução às EDO'sLista de Subespaços VetoriaisLista de ElipsesLista de Parábolas Lista de Ângulos entre RetasLista de Combinação LinearLista de Posições Relativas de RetasLista de Expressão Analítica de uma TLLista de Reflexão OrtogonalLista de Escalonamento

Principais Conceitos de Álgebra Linear e Geometria Analítica

Equação da Esfera