Sejam e . Nos casos do exercício anterior, obtenha equações do lugar geométrico dos pontos médios dos segmentos paralelos a com uma extremidade em e outra em . Descreva o lugar gométrico.

(a) e

Qualquer ponto no plano com certeza satisfaz essa relação aqui:

Vamos usar essa equação para parametrizar o plano:

E qualquer ponto no plano satisfaz essa relação aqui:

E agora vamos fazer a mesma coisa para o plano :

Beleza, já sabemos a forma geral de e .

Agora que sabemos isso, vamos procurar a forma geral do ponto médio . Esse é o ponto médio de um segmento qualquer que vai de até .

Ok, agora também temos a expressão do ponto médio. Para saber o que fazer agora, vamos fazer o desenho mais uma vez:

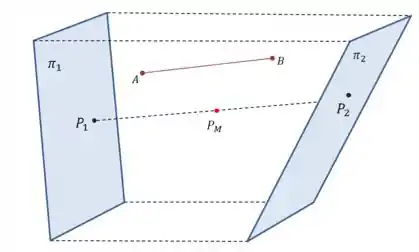
Nessa questão, a gente está preocupado com os pontos médios dos segmentos que são paralelos a .

Como a gente pode escrever isso matematicamente? O segmento é:

Vamos ver como isso se relaciona com o ponto médio:

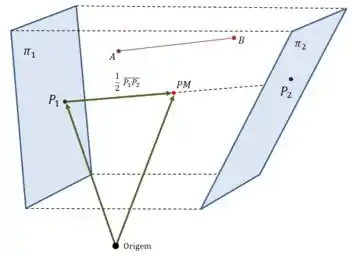
Olhando um pouco para o desenho, podemos escrever:

E se esse segmento é paralelo a , então ele é um múltiplo do segmento :

Então podemos substituir na equação de cima:

Beleza, essa é a equação que a gente quer resolver para encontrar .

Lembrando que é:

Então vamos escrever essa equação com as expressões que temos lá em cima:

As equações são:

Então tá, temos aí variáveis ( e ), e equações (uma para cada coordenada).

Com isso podemos escrever um sistema:

E esse sistema vai ter dois graus de liberdade , então vamos ter duas variáveis livres na resposta final.

E a gente quer resolver isso para reescrever a equação de , que é a resposta que procuramos.

Vamos primeiro simplificar a última equação:

Multiplicando tudo por :

Agora é só reorganizar:

Então:

E multiplicando as duas primeiras equações por :

E simplificando as duas primeiras também:

Agora vamos começar a resolver o sistema:

Escrevendo na forma matricial:

E na forma escalonada:

Vamos começar zerando o na terceira linha:

Agora vamos multiplicar a segunda linha por e fazer:

Agora vamos multiplicar a terceira linha por :

E agora somar a terceira linha à primeira:

Então voltando ao sistema linear:

Beleza, conseguimos deixar a situação com só graus de liberdade.

Como falamos antes, vamos substituir lá na fórmula do :

Temos que substituir , e . Vamos escrever em forma de matriz-coluna para deixar menos bagunçado:

As duas primeiras linhas são mais tranquilas:

A última é um pouco mais trabalhosa:

Agora é só somar os termos com coeficientes iguais:

E então:

Calma, estamos quase lá, agora só precisamos encontrar o plano que esse conjunto de pontos gera.

A gente espera que seja um plano porque temos dois graus de liberdade e ).

A gente já tem as equações paramétricas do plano. Lembra como faz para encontrar a equação geral a partir disso?

Outra forma de escrever isso é:

Para encontrar a equação geral desse plano, é só tirar o determinante dessa matriz aqui e igualar a zero:

Onde são as constantes, e e são os vetores diretores, então:

Calculando o determinante dessa matriz, ficamos com o seguinte:

E multiplicando tudo por :

Finalmente! Encontramos a equação do plano que estávamos procurando!