Enunciado
Álgebra Linear e Geometria Analítica - Alfredo Steinbruch e Paulo Winterle - Geometria Analítica- Ed: 1º - Capítulo 5.Problemas Propostos - Ex. 41h
Seja o paralelepípedo de dimensões e , representado a seguir.
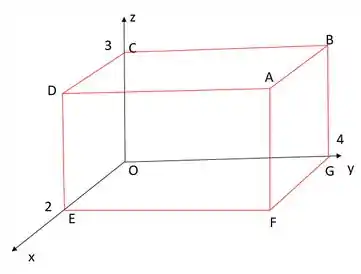
Determinar a equação do plano que contém a face ABGF
Passo 1
Para essa questão, precisamos tomar um vetor normal à face ABGF para termos as coordenadas Quando acharmos, vamos jogar na equação
E encontrar a equação do plano.
Passo 2
A face ABGF está apoiada no plano , portanto, o vetor normal a essa face é o versor
. Assim, temos
Passo 3
Para acharmos o termo , podemos substituir por qualquer um dos pontos que compõem a face ABFG. No caso, vamos substituir com o ponto . Dessa forma, temos
Com todos os termos, temos então a equação
Ou
Pronto, chegamos ao fim da questão
Resposta
ou
Exercícios de Livros Relacionados
Obtenha equações do lugar geométrico dos pontos médios dos segmentos com uma extremidade em r e outra em s e descreva-o geometricamente.(c) r : X = 1 ,0 ,0 + λ - 1 ,0 ,1 s : X = 0 ,0 ,1 + μ ( 2 ,1 ,1
Obtenha equações do lugar geométrico dos pontos médios dos segmentos com uma extremidade em r e outra em s e descreva-o geometricamente.(a) r : X = 1 ,2 ,2 + λ 0 ,1 ,1 s : X = 0 ,0 ,0 + μ ( 1 ,0 ,1 )
Sejam π 1 : a 1 x + b 1 y + c 1 z + d 1 = 0 e π 2 : a 2 x + b 2 y + c 2 z + d 2 = 0 planos transversais, e r sua interseção.(c) Conclua que a 1 x + b 1 y + c 1 z + d 1 + λ a 2 x + b 2 y + c 2 z + d 2
Sejam π 1 : a 1 x + b 1 y + c 1 z + d 1 = 0 e π 2 : a 2 x + b 2 y + c 2 z + d 2 = 0 planos transversais, e r sua interseção.(a) Mostre que, para todo plano π que contém r e é diferente de π 2 , existe
Sejam π 1 : a 1 x + b 1 y + c 1 z + d 1 = 0 e π 2 : a 2 x + b 2 y + c 2 z + d 2 = 0 planos transversais, e r sua interseção.(b) Mostre que não existe λ real tal que π 2 : a 2 x + b 2 y + c 2 z + d 2 +