Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Um curso de geometria analítica e álgebra linear, Reginaldo J. Santos- Ed: 1º - Capítulo 3.1 - Ex. 18b

Sejam A ,   B e C pontos quaisquer com A ≠ B . Prove que:

b) Um ponto X pertence ao interior do segmento A B ( A X → = λ A B → , com 0 < λ < 1 se, e somente se, C X → = α C A → + β C B → ,

com α > 0 ,   β > 0 e α + β = 1 .

Passo 1

Na última alternativa mostrando algumas coisinhas que vão ser úteis para esta questão, nós temos que:

X = λ A B → + A

E também que α = 1 - λ e β = λ , tal que:

α + β = 1

Vamos tentar usar isso aqui!

Passo 2

Se testarmos os limites para λ , temos que:

λ = 0 → α = 1   e   β = 0

Portanto, temos que

C X → = C A →

Observe o seguinte esquema:

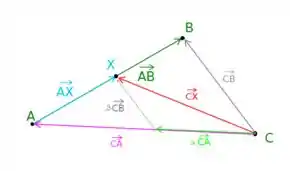
Ou seja, X = A . Algo parecido acontece se λ = 1 , temos que α = 0 e β = 1 , e agora temos que:

C X → = C B →

E podemos ver que X = B . O que isso quer dizer então?

Passo 3

Quer dizer que se temos 0 < λ < 1 , então necessariamente temos que:

β = λ → 0 < β < 1

E também que, se:

α = 1 - λ → λ = α - 1 → 0 < α - 1 < 1 → 1 < α < 2

Portanto, sim, é necessário que β > 0 , e também que α > 1 > 0 . Essa foi a segunda alternativa, bora para a última!

Resposta

Ao longo dos passos!

Exercícios de Livros Relacionados

Determine uma equação da esfera que passa pela origem e tem centro (1, 2, 3).
Se alpha U = alpha V , então U = V ? E se alpha != 0 ?
Sejam A ,B e C pontos quaisquer com A ≠ B . Prove que:c) Um ponto X é um ponto interior ao triângulo A B C ( A ' X → = λ A ' B ' → ,c o m0λ1 , em que A ' é um ponto interior ao segmento A C e B ' é in
Sejam A ,B e C pontos quaisquer com A ≠ B . Prove que:a) Um ponto X pertence a reta determinada por A e B ( A X → = λ A B → ) se, e somente se, C X → = α C A → + β C B → com α + β = 1 .