Sejam A ,B e C pontos quaisquer com A ≠ B . Prove que:c) Um ponto X é um ponto interior ao triângulo A B C ( A ' X → = λ A ' B ' → ,c o m0λ1 , em que A ' é um ponto interior ao segmento A C e B ' é interior ao segmento C B ) se, e somente se, C X → = α C A → + β C B → , Com α0 , β0 e α + β1 .

Enunciado

Álgebra Linear e Geometria Analítica - Um curso de geometria analítica e álgebra linear, Reginaldo J. Santos- Ed: 1º - Capítulo 3.1 - Ex. 18c

Sejam e pontos quaisquer com . Prove que:

c) Um ponto é um ponto interior ao triângulo (, em que é um ponto interior ao segmento e é interior ao segmento ) se, e somente se,

Com , e .

Passo 1

Na alternativa anterior nós mostramos que e caso quiséssemos analisar um ponto sobre o segmento entre os pontos e . Esta situação é representada pelo seguinte:

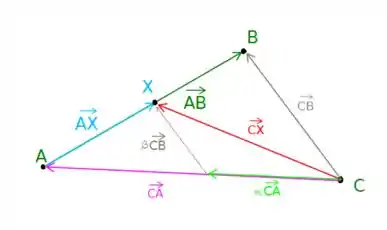
Esta situação foi estabelecida levando em conta que . Vamos tentar divagar um pouco em cima disso!

Passo 2

Como temos que , temos que , portanto:

Ou seja

Só que lembrando que , temos que e também que . Ou seja:

Os vetores e são colineares. O que acontece, no entanto, se

Passo 3

A seguinte expressão

O vetor . Também, o vetor , ou seja, temos a seguinte situação:

A questão foi isso! Te vejo na próxima!! Tchauzinho!

Resposta

Ao longo dos passos!

Exercícios de Livros Relacionados

Dados A B → = a → , B C → = b → e C D → = c → , determine, em função de a → , b → e c → , os vetores A X → e F X → , sabendo que E X → = 1 4 E B → .

Dado um tetraedro OABC, tem-se O A → = a → , O B → = b → , O C → = c → , O P → = 2 3 O B → . M é o ponto médio de A B → , N é o ponto médio de B C → e Q é o ponto médio de A C → . Pede-se u → = P M →

Dados os vetores u →=( 0,1 , - 1 ) e w →=( 2,5 , 4 ) , calcule o comprimento da projeção do vetor - 4 u →+w → sobre o eixo cuja direção é dada pelo vetor w → - 2 u → .

No triângulo ABC, P, Q e R são os pontos médios, respectivamente, de AB, BC, e AC. O ponto O é um ponto qualquer do espaço. Demonstre: O A→ +O B→ +O C →=O P →+O Q→ +O R →. (Sugestão: escreva O P → , O

Prove que o segmento que une os pontos médios de dois lados de um triângulo é paralelo ao terceiro lado e tem comprimento igual à metade do comprimento desse lado.