Enunciado
Álgebra Linear e Geometria Analítica - Um curso de geometria analítica e álgebra linear, Reginaldo J. Santos- Ed: 1º - Capítulo 3.1 - Ex. 18a
Sejam e pontos quaisquer com . Prove que:
a) Um ponto pertence a reta determinada por e se, e somente se,
com
Passo 1
Oiii, tudo bem? Bora para mais uma?
Para resolver esta questão vamos lembrar algumas coisinhas! Primeiro, se temos que o ponto está sobre a reta que passa por , que formam o vetor , como no seguinte esquema:
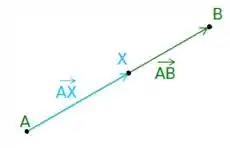
Note que o vetor , e como ambos os vetores são colineares devem obedecer a uma relação do tipo:
Um ponto , obedece a seguinte relação:
Beleza, mas o que faço com isso? Saca só!
Passo 2
Podemos escrever o vetor , então;
O que podemos expandir da seguinte maneira:
Vamos precisar utilizar de um truquezinho aqui! Bora lá!
Passo 3
Se somarmos e subtrairmos nos parênteses o ponto C, temos:
Podemos reorganizar as coisas um pouquinho:
Colocando o vetor em evidência, temos:
Portanto, temos finalmente que se e , temos:
Como queríamos demonstrar, vamos para a próxima alternativa agora!
Resposta
Ao longo dos passos!