Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Complemento Ortogonal e Soma Direta

Ver Todos os Exercícios

Teoria

Opaa, seja bem vindo ao Responde Aí! Bora bater um papo sobre soma direta de subespaços? Mas antes de qualquer coisa…vamos dar uma breve revisada sobre complemento ortogonal…

O que é Complemento Ortogonal?

Ortogonal nada mais é do que um nome metido a besta para coisas perpendiculares! Por exemplo, se a gente tem duas retas que se interceptam formando um ângulo de podemos dizer que elas são ortogonais!

Beleza, então vamos a definição de complemento ortogonal:

Seja um subespaço vetorial. O complemento ortogonal de é o conjunto $V^{\perp} =\{ w \in R^n | .

O que essa definição super formal aí esta dizendo pra a gente é que, se temos um conjunto qualquer, então o complemento ortogonal de vai ser um outro conjunto com em que TODOS os elementos são ortogonais a .

Por exemplo, vamos pegar considerar que esteja no e seja o plano . Quem será o seu complemento ortogonal?

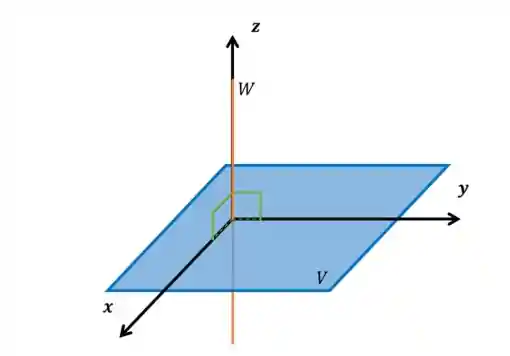
Complemento ortogonal de um plano
Complemento ortogonal de um plano

Nesse caso o plano ortogonal de será o próprio eixo , afinal todos os seus elementos são perpendiculares ao plano !

📢 Clique para ver mais:

Como Calcular o Complemento Ortogonal por Soma Direta?

Beleza…mas vamos supor que quiséssemos, por exemplo, saber o complemento ortogonal de um plano no ?! 😱😱😱

É aí que entra a soma direta!

Nesse vídeo abaixo eu te explico tudo o que você precisa saber sobre soma direta! Dá uma conferida! 👇

Soma direta de um Subespaço

Vamos ao que interessa! O que é a soma direta de um subespaço e qual é a sua relação com complemento ortogonal?!

A soma da dimensão de um subespaço com a dimensão do seu complemento ortogonal é igual a dimensão do espaço em que estão contidos.

Vamos aplicar essa definição ao exemplo lá de cima onde queríamos saber o complemento ortogonal de um plano no . Sabemos que o plano tem dimensão e o tem dimensão . Então o complemento ortogonal de um plano no terá dimensão:

Maneiro, não?! Daí que vem o nome “complemento”. Ele de fato complementa as dimensões que faltavam para ocupar todo o espaço! Sempre que nós pegarmos uma base de um conjunto e juntar com a base do complemento ortogonal , teremos uma base do !

Agora vamos praticar com exercícios?

Exercícios Resolvidos

Exercício Resolvido #1

UFRJ-P4-2015.2.1

Seja H o conjunto dos vetores do R 4 cuja soma das duas primeiras coordenadas é zero. Então H ⊥ , o complemento ortogonal de H , é:

a   Um plano

b   Um hiperplano

c   O R 4

d   Uma reta

Passo 1

Vamos lá!

Sabemos que H é formado por:

x + y = 0 ⇒ x = - y

x , y , z , w = - y , y , z , w = y - 1,1 , 0,0 + z 0,0 , 1,0 + w ( 0,0 , 0,1 )

Sendo assim podemos ver que temos 3 vetores L I e, portanto, a dimensão é 3 . Logo como sabemos que:

dim ⁡ H + dim ⁡ H ⊥ = dim ⁡ R 4

Podemos ver que a dimensão do complemento deve ser uma reta, pois deve ter dimensão 1 :

3 + dim ⁡ H ⊥ = 4 ⇒ dim ⁡ H ⊥ = 1

Resposta

Letra d

Exercício Resolvido #2

UFRJ-P3-2012.1

Seja V um espaço vetorial de dimensão 5 .

Seja H um subespaço gerado por 3 vetores não nulos de V .

Então a dimensão do complemento ortogonal de H pode ser no máximo igual a 4 .

a   A afirmativa é falsa.

b   A afirmativa é verdadeira.

Passo 1

Sabemos que a dimensão de H e a dimensão de seu complemento ortogonal H ⊥ somadas têm que dar 5 .

Logo afirmar que a dimensão de H ⊥ é no máximo igual a 4 dá no mesmo que afirmar que a dimensão de H é no mínimo igual a 1 .

E isso é verdade!

Se um vetor é não-nulo, então o espaço gerado por ele tem dimensão 1 .

Mas pode ser que eu escolha mais 2 vetores não nulos para H que sejam todos paralelos ( L D ).

Se isso acontecer, a dimensão do espaço será 1 , que é o valor mínimo. Nesse caso, H ⊥ terá dimensão 4 .

Resposta

Letra b

Exercício Resolvido #3

PUCRIO-P3-2014.1-2a

Verdadeiro ou Falso? Forneça uma justificativa para sua resposta.

“Se R n é soma direta dos subespaços H e W , então W é o complemento ortogonal de H . Noutras palavras, se R n = H ⊕ W , então W = H ⊥ . (Lembre: R n = H ⊕ W se, e somente se, R n = H + W , H ∩ W = 0 . ”

Passo 1

Falso

Podemos justificar pegando um exemplo no R 3 . Pegue o plano x y :

H = x y = s p a n { 1,0 , 0 , 0,1 , 0 }

E assim seu complemento ortogonal seria o próprio eixo z . Mas não necessariamente ele satisfaz o fato de ser soma direta com o plano x y .

Passo 2

Assim, podemos pegar um outro conjunto formado por:

W = s p a n 0,1 , 1

Sabemos que, para estes H e W , R n = H ⊕ W , mas H ⊥ ≠ W .

OBS: Outros exemplos também são possíveis.

Resposta

Falso.

Exercício Resolvido #4

PUCRIO-P4-2015.1-1 - b)

À questão “No espaço R 3 munido do produto interno usual, calcule o complemento ortogonal de H = s p a n { 1 , 1,1 } ”, Biazinha escreveu:

Sem mostrar a resposta correta para Biazinha, como você a convenceria que resposta está errada?

Passo 1

Como H é um espaço de dimensão 1 no R 3 , então seu complemento ortogonal deve ter dimensão 2 já que:

H ⊕ H ⊥ = R n

Assim, podemos ver que Biazinha achou um complemento ortogonal de dimensão 1 , e sem verificar as contas, já podemos ver que sua resposta está errada.

Resposta

Ei, a resposta está no passo a passo :)

Exercício Resolvido #5

PUCRIO-P4-2014.2

Andrezinho respondeu à questão “Prove que, para todo subespaço vetorial H ⊂ R n , tem-se que H ⊕ H ⊥ = R n " da seguinte maneira:

Complete a demonstração do Andrezinho. (Use as dimensões de H e H ⊥ !)

Passo 1

Ficou faltando na demonstração provar que H + H ⊥ = R n , mas... como provar??

Bom, já sabemos que H ⊂ R n e H ⊥ ⊂ R n , ou seja, H e H ⊥ possuem os mesmos elementos e operações de R n . Então, basta provar que as dimensões da soma dos dois subespaços são iguais ao do R n .

Pela fórmula das dimensões sabemos que:

dim ⁡ H + H ⊥ = dim ⁡ H + dim ⁡ H ⊥ - dim ⁡ ( H ∩ H ⊥ )

Passo 2

-

Mas como a interseção é zero...

dim ⁡ H + H ⊥ = dim ⁡ H + dim ⁡ H ⊥

E como sabemos que:

d i m ( H ) = k

dim ⁡ H ⊥ = n - k

dim ⁡ H + H ⊥ = k + n - k = n = d i m ⁡ ( R n )

E assim, podemos dizer que H + H ⊥ = R n .

Resposta

Ei, a resposta está no passo a passo :)