Reflexão Ortogonal
Teoria
Já aprendemos a projetar vetores em um espaço. O próximo passo naturalmente será vermos como refletir um vetor em torno de um espaço qualquer.
Novamente, vamos ficar na parte matemática da coisa, tentando imaginar ou visualizar o mínimo possível. Essa preparação é essencial, pois se você se encontrar com um problema acima do tentar visualizar não valerá de nada.
Encontrando a TL da Reflexão
Novamente, vamos ver o que acontece com um vetor pertencente à , o plano , reflexionado em torno de , e um vetor pertencente ao seu complemento ortogonal reflexionado em torno de .
Observe a figura:
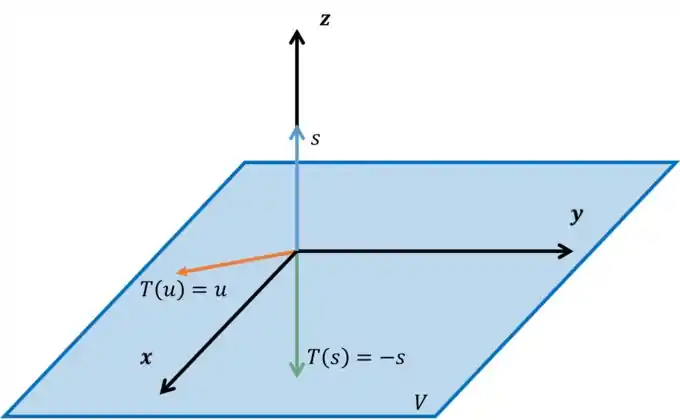
Veja que se pegarmos um vetor pertencente à e o refletirmos em torno de , dará o próprio vetor (pense como se fosse um espelho!). Agora, se pegarmos um pertence ao complemento ortogonal, é só você inverter seu sentido!
Assim, vamos usar a mesma ideia da projeção. Fica muito intuitivo de entender isso no , mas vamos generalizar para todos os espaços com uma transformação linear e nossa transformação fica assim:
Obs: Para montar a reflexão, é só fazer a mesma coisa que sempre fizemos, defina uma base pro domínio, aplique em cada um dos vetores... No caso da reflexão e da projeção é muito fácil achar a imagem dos vetores da sua base, pois basta definir a base com os vetores de e , e juntar para ter a do !
O procedimento será quase idêntico ao que usávamos na projeção, mas vamos ver um exemplo.
Vamos calcular a que reflete um vetor do em torno da reta .
Passo 1: Encontrar uma base para o espaço em torno do qual se quer refletir e para seu complemento ortogonal.
Pela equação da reta temos:
Logo, o vetor genérico é dado por . Então uma base para esse subespaço seria:
O complemento ortogonal será a reta perpendicular à essa, e tem como base:
Com isso, chegamos à base do :
Qualquer vetor do pode então ser escrito como:
Passo 2: A imagem da base do espaço em torno do qual se quer refletir, será a própria base. A imagem da base do complemento ortogonal será o vetor com o sentido trocado.
Aplicando a transformação em ambos os lados da igualdade e usando do fato acima temos:
Passo 3: Para encontrarmos a equação da precisamos dos valores de e . Então:
Resolvendo o sistema, temos:
Passo 4: Substituímos na equação da :
E temos nossa .
Matriz que representa a
Novamente, nenhum mistério para achar a matriz da acima. Basta separarmos ela:
Logo, nossa matriz é:
Essa matriz como já vimos lá em projeção está na base canônica. Analogamente se quisermos , onde é a base formada pela base do subespaço em torno do qual estamos refletindo e pela base de seu complemento ortogonal, teremos:
Note que novamente temos uma matriz diagonal. Perceba também que o primeiro vetor da base tem como imagem ele mesmo, daí o número como primeiro valor na diagonal. Já o segundo vetor da base tem como imagem ele mesmo com o sentido invertido, então temos o como segundo valor na diagonal.
Bizus
Assim como na matriz projeção, eu tenho uns bizus muito bons pra passar pra vocês sobre a matriz reflexão!
A inversa da matriz reflexão será sempre ela mesma!! Se pensarmos bem até que faz algum sentido não acha?
Se você reflete um vetor em torno de um espaço, e depois reflete de novo em torno do mesmo espaço, você têm que obter o mesmo vetor né!
E disso temos outra aplicação. Se você tiver uma memória muito poderosa deve se lembrar de quando eu falei lá atrás em matrizes ortogonais. Lá eu falei que toda matriz reflexão é ortogonal, ou seja, possui a inversa igual à transposta.
E como sabemos que uma matriz reflexão é igual a sua inversa, chegamos à conclusão de que ela também é igual à sua transposta!!!!
Então temos que se é uma matriz reflexão qualquer,
E por fim, assim como para a matriz projeção, também temos uma relação entre o traço da matriz e o espaço no qual estamos projetando! Só que aqui a relação é beeeem mais bizarra. Bom, se você pega o traço de uma matriz reflexão, soma a dimensão do domínio da matriz e divide esse valor por , você vai ter a dimensão do espaço em torno do qual ela reflete :p
Por exemplo, se for uma reflexão no e o traço da matriz é , temos:
Ou seja, ela reflete por uma reta! Não acho que seja interessante explicar o motivo disso, mas ta aí né haha.
Matriz que representa a T L
Bizus
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
Determine as matrizes das :
reflexão em torno da reta
, reflexão em torno do plano
Passo 1
É pedida a matriz que representa a reflexão em torno da reta . Primeiro vamos achar o vetor gerador da reta. Temos:
Logo os vetores da reta são da forma
Portanto, um vetor gerador possível é o
O complemento ortogonal dessa reta é o subespaço gerado pelo vetor
Com isso, chegamos à base do :
Qualquer vetor do pode então ser escrito como:
Aplicando a transformação em ambos os lados da igualdade:
Passo 2
Agora precisamos encontrar e em função de e :
Fazemos :
Substituindo em
Passo 3
Substituindo na equação da :
Abrindo a , temos:
Logo, a matriz é dada por:
Passo 4
Agora precisamos da matriz que representa reflexão em torno do plano . Os vetores desse plano obedecem a seguinte restrição:
O vetor genérico desse plano tem a forma:
Uma base para ele seria então:
Onde:
Seu complemento ortogonal é a reta cujo gerador pode ser dado pela equação do plano:
Onde
Temos então uma base para o :
Logo,
Passo 5
Aplicando a transformação em ambos os lados:
Precisamos descobrir e em função de e :
De temos que:
De temos que:
Substituindo e em :
Substituindo em e em :
Passo 6
Substituindo na equação da :
Desmembrando a transformação:
Logo, temos que:
Resposta
Exercício Resolvido #2
Lista2 para a p2, Álgebra Linear I, 2015.1, exercício 10, PUC-rio.
Sejam uma base de e uma base de . Sejam também e as transformações de projeção e reflexão ortogonal em relação a respectivamente. Calcule e onde .
Passo 1
Primeiro vamos definir as bases do enunciado. Vamos chamar e como é base do complemento ortogonal de , é a continuação direta da base de , . E assim nossa base do é:
Passo 2
Pronto! Agora é só montar a matriz, que já estamos acostumados a montar! Vamos fazer primeiro a da projeção.
Vamos aplicar a nos vetores da base que são de , e depois os que são de .
Já que é base de :
Já que é base de :
Passo 3
Agora que já temos a imagem dos nossos vetores da base, só falta reescrevê-los na própria base . Mas como pertencem à base , a primeira parte da nossa matriz ficará assim:
Agora como o resto deu zero, a nossa matriz vai ficar assim:
Passo 4
A mesma ideia vamos aplicar à transformação reflexão. Então, vamos calcular as imagens dos vetores da base do nosso domínio:
Já que é base de .
Passo 5
Agora observe que os vetores da imagem compõem também a base , e assim fica bem fácil de escrever a nossa matriz! Primeiro, vamos fazer a matriz até os vetores da base de .
Agora vamos fazer até :