Calcule a taxa de Nyquist para os sinais abaixo:
Passo 1
Para calcular a taxa de Nyquist, precisamos saber a frequência do sinal. Para a função cosseno, assim como para a função seno, a frequência é dada pelo argumento da função. Ou seja:
A frequência da função, em é igual a .
Para a letra a) teremos então:
Passo 2
Como estamos em busca da taxa de Nyquist, essa medida é mais comumente dada em (amostras por segundo). Para fazer a mudança de unidade usaremos:
Onde é a frequência em e é a frequência em .
Vamos então encontrar a frequência do nosso sinal em :
Passo 3
Agora só falta encontrar a taxa de Nyquist.
A taxa de Nyquist é igual ao dobro da frequência máxima de um sinal. Como aqui só temos uma frequência, a taxa de Nyquist para a letra a) será:
Passo 4
Para o item b), podemos perceber que se trata da mesma função, porém multiplicado por uma constante.
A função cosseno quando multiplicada por uma constante não terá sua frequência alterada, apenas a sua magnitude. Os gráficos abaixo demonstram isso:
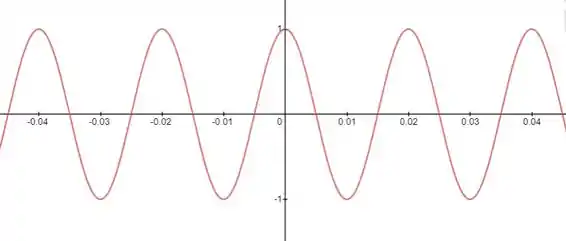
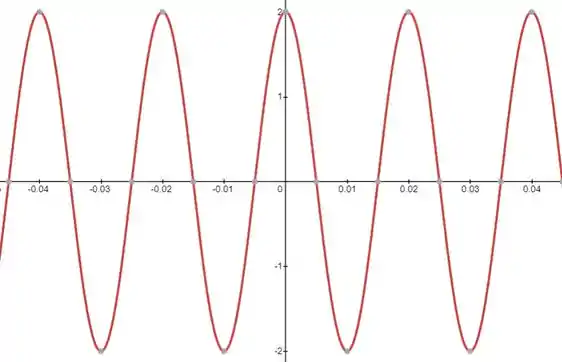
Os gráficos mostram os sinais da letra a) e b) respectivamente. Perceba que devido à multiplicação pela constante, a amplitude do sinal (tamanho dos picos e vales) dobrou, mas a frequência (quantidade de ciclos) num mesmo intervalo se manteve a mesma.
Portanto, a frequência do sinal não mudou e portanto a taxa de Nyquist para esse sinal também não mudará:
Passo 5
Para a letra c) teremos novamente o mesmo sinal, porém dessa vez, elevado ao quadrado.
Quando elevamos a função cosseno ao quadrado, toda a parte negativa dessa função será refletida para o eixo positivo:
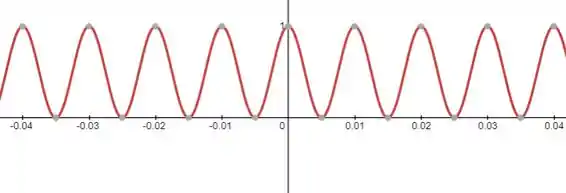
Podemos perceber que quando comparamos o gráfico do sinal do item c) com o do item a) a frequência foi dobrada (dobrou a quantidade de ciclos), portantoa taxa de Nyquist também será dobrada: