Dado o sinal abaixo, qual seria a frequência do sinal discreto caso o sinal seja amostrado a uma taxa de .
Passo 1
Para resolver essa questão, vamos usar o gráfico do sinal para facilitar a visualização:
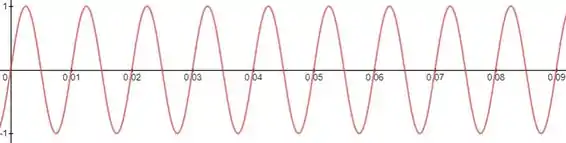
Perceba que o tempo que o sinal demora para completar um ciclo completo é de , fazendo com que a frequência seja de :
Esse valor é condizente com o valor que encontraríamos pela expressão do sina pois:
Passo 2
O sinal será amostrado a uma taxa de . O que quer dizer que a cada segundo, amostras serão colhidas.
Vamos determinar quanto tempo leva para colher cada amostra:
Ou seja, a cada segundos, uma amostra é feita.
Passo 3
Vamos fazer a amostragem usando o gráfico da função acima e uma amostra a cada segundos:
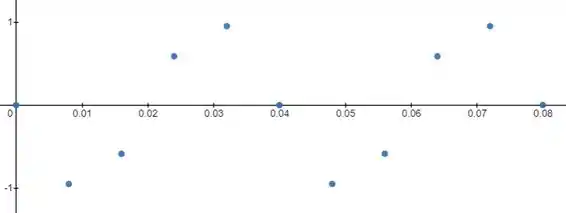
Passo 4
Repara que o ciclo começa em só se conclui em . Podemos calcular a frequência do sinal amostrado então:
Que é uma frequência oito vezes menor do que a frequência do sinal contínuo. Isso aconteceu porque a amostragem foi feita numa taxa menor que a taxa de Nyquist. Para esse caso a taxa de Nyquist seria:
Ou seja, qualquer amostragem que fosse feita a uma taxa superior a a frequência do sinal amostrado seria igual à do sinal contínuo. Como a taxa de amostragem foi menor, a frequência não foi a mesma. Isso é o que chamamos de aliasing.