Calcule o valor da potência útil ao se reduzir pela metade o valor do número de rotações de rotações do impelidor referente a um tanque com chicanas. As únicas informações disponíveis do sistema original são:
Passo 1
Essa questão é um exemplo de que não necessariamente precisa mudar o tanque para mudar a escala. Aqui a escala foi mudada devido à mudança do número de rotações do impelidor.
E repara que, ao mudar o número de rotações, estamos mudando também o número de Reynolds do impelidor, já que:
E, ao mudar o Reynolds do impelidor, há mudança fluidodinâmica no sistema.
Algo que temos que notar é que há semelhança geométrica nas duas situações, até porque nem chegamos a mudar o tanque.
Para a mudança de escala, vamos usar a semelhança fluidodinâmica.
Passo 2
Na situação original, o número de Reynolds era
Com:
Como o número de rotações, , que é diretamente proporcional a , foi reduzido pela metade, o novo Reynolds será:
Dando uma olhada na curva b do gráfico para curva de potência, já que o impelidor é de pás retas e há chicanas no tanque.
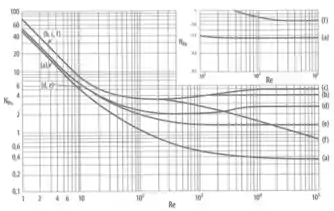
Vemos que esse valor de número de Reynolds corresponde a regime turbulento. Daí, a semelhança fluidodinâmica pode ser expressa por:
Como o fluido do processo é o mesmo nos dois casos, a densidade, , é a mesma. Ficamos com:
E, como o diâmetro do impelidor é o mesmo nos dois casos, podemos cortar os também”
Passo 3
Como estamos interessados na potência útil no caso 2, bora isolar esse termo:
O enunciado diz que o número de rotações foi reduzido pela metade, daí:
Substituindo isso, ficamos com:
E agora é só fazer conta haha Como na situação inicial :