Calcule a área específica em volume de uma casca cilíndrica cujas especificações são:
Passo 1
Bora primeiro entender melhor essa geometria: casca cilíndrica é como se você tirasse um cilindro de dentro de um cilindro. Aí tem um buraco no meio. Tipo assim:
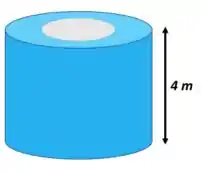
Esse buraco vai de uma ponta até a outra aí a vista superior fica assim, olha:
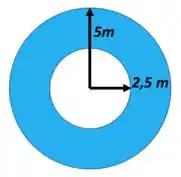
Temos que calcular a área específica em volume, :
Daí, vamos precisar calcular a área superficial e o volume dessa casca cilíndrica.
Passo 2
Bora começar calculando a área superficial.
A superfície da casca cilíndrica inclui a área lateral externa (), área lateral interna (), anel da base () e anel do topo ().
Calculando um por um:
A área lateral externa é a área lateral de um cilindro: perímetro da base multiplicada pela altura. Como o perímetro da base é uma circunferência:
Já que e :
A área lateral interna é calculada de forma semelhante, já que a lateral interna também tem forma cilíndrica:
A altura é a mesma, , mas :
A área da base é um anel; a área do anel é a área do circulo maior menos a área do circulo menor, ou seja:
Substituindo os valores:
E repara que a base é igual ao topo, daí as áreas são iguais:
Somando tudo:
E não podemos esquecer da unidade! Como trabalhamos com todos os comprimentos em metros, a unidade da área é :
Passo 3
Agora precisamos do volume dessa casca cilíndrica. A fórmula para volume é:
Já calculamos a área da base e já temos a altura: e .
Substituindo os valores:
Não esquecendo da unidade:
Passo 4
Temos e . Agora é só dividir um pelo outro e teremos o , em :