Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Diferenciação Numérica

Ver Todos os Exercícios

Teoria

Teoria pra que te quero?

Opa, tudo bem? O conteúdo que vamos entender agora não é estudado em todas as Universidades, então se você não tem esse conteúdo na sua grade... é só passar para o próximo tópico que fica tudo bem!

Consegue imaginar sobre o que vamos estudar?

Ah... qual é, essa dica é boa haha

E agora?

O queijo é derivado do? leite hahahahah vamos falar de derivadas, der!

Vamos começar a estudar sobre diferenciação numérica. Sabe, na vida real nós lidamos o tempo todo com η situações que variam e para isso, temos que estar preparados para lidar com essas mudanças.

Por exemplo, quando falamos de taxa de variação, queremos falar sobre derivadas e que significa justamente a taxa na qual uma grandeza varia em função de outra grandeza e pode ser dada por:

d f d x = lim Δx → 0 ⁡ f x i + Δ x - f ( x i ) Δ x

E esse, é um conceito que nós obtemos láaaaaaaaaaaaaaaaaaaaaaaaaaaaaa em Cálculo 1. Onde temos x (como variável independente) e f x = y (como variável dependente). Até aí tudo ok né?

Em alguns casos a derivada é complicadinha demais para resolver analiticamente. Tipo essa aqui:

f x = e x + ln ⁡ sin ⁡ x 2 + a r c t g   1 + x 3 1 2 + cos ⁡ 42 x . s e n 35 x 2 + 1 x

É, definitivamente precisamos de uma ajudinha extra quando solucionamos esse tipo de derivada!

Tem algumas derivadas cabulosas mesmo Hahahaha! E é aí que surge a necessidade de utilizar a derivação numérica.

Para solucionar o problema das derivadas difíceis podemos usar duas abordagens: conhecer a função a ser derivada ouuuuuuuuuu ter um conjunto de pontos (geralmente representados como tabela de valores). O problema de usar esses conjuntos de pontos é que a resolução do problema acaba se limitando a quantidade de dados disponíveis.

A diferenciação numérica é também conhecida como aproximação numérica e é usada para aproximar e avaliar algumas derivadas, aquelas que tem um conjunto de pontos. Esse tipo de aproximação pode ser feito usando uma interpolação polinomial. Que por definição:

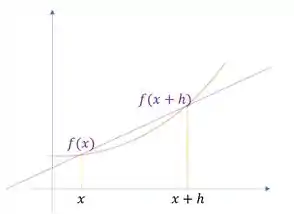
E se trata de uma abordagem interessante, para achar a derivada no ponto x * , nós determinamos um polinômio interpolador p ( x ) a partir de valores f em pontos próximos a x * e assim conseguimos estimar a f ' ( x * ) pela derivada do polinômio p ' x * . Essa abordagem costuma ser usada quando usamos um conjunto de pontos que não são igualmente espaçados.

Quando a função f ( x ) é conhecida em um conjunto de pontos igualmente espaçados, usamos outras técnicas como o cálculo de derivadas usando as operações de diferenças finitas.

Diferenças finitas

Diferença finita é uma expressão da forma f ( x + b ) - f ( x + a ) , que ao ser dividida por ( b - a ) chama-se um quociente de diferenças. Essa técnica serve para aproximar a derivada de uma função via fórmulas discretas que requerem apenas um conjunto limitado de pares ordenados x i , y i } i = 1 n onde geralmente denotamos y i = f ( x i ) .

Fórmula das diferenças superior

Pode ser chamada de Diferença superior ou progressiva. É uma das abordagens de diferenças finitas que se dá pela seguinte fórmula:

D h f x = f x , x + h = f x + h - f ( x ) h

Quando:

h = x 1 - x 0

Se:

x = x 0

Então a diferença é progressiva.

Fórmula das diferenças inferior

Pode ser chamada de Diferença inferior ou regressiva. É uma das abordagens de diferenças finitas que se dá pela seguinte fórmula:

D h f x = f x , x - h = f x - f ( x - h ) h

Se:

x = x 2

Então a diferença é regressiva.

Fórmula das diferenças centrada

Esse, é um caso intermediário e por isso recebe o nome de “centrado”. Isso significa que pega um pouco da progressiva e regressiva. Sua fórmula é a seguinte:

D h f x = f x - h , x + h = f x + h - f ( x - h ) 2 h

Onde:

h = x 1 - x 0 2

Se:

x = x 1

Erros

Consideramos f ( x + h - ) a representação em ponto flutuante.

Diferenças finitas

Fórmula das diferenças superior

Fórmula das diferenças inferior

Fórmula das diferenças centrada

Erros

Exercícios Resolvidos

Exercício Resolvido #1

Adaptado de “Derivação e Integração numérica- Professor Renan G. P. Soares “

Dado a função f x = l n ⁡ ( x ) , calcular a derivação numérica com a fórmula da diferença superior para x = 1,8   e h = 0,1 . Além disso, considere o valor real da derivada obtido no ponto dado e compare com o valor obtido.

Passo 1

A primeira consideração a ser feita é a que essa é uma integral fácil de se calcular:

f x = l n ⁡ ( x )

f ' x = 1 x

Se x = 1,8 :

f ' ( 1,8 ) = 1 1,8 = 0,555554

Passo 2

Agora, conseguimos encontrar a derivada pelo método das diferenças superior, usando a fórmula dada:

D h f x = f x , x + h = f x + h - f ( x ) h

Se x = 1,8 ; h = 0,1 :

D h f x = f x , x + h = f 1,8 + 0,1 - f ( 1,8 ) 0,1

D h f x = f x , x + h = l n ⁡ ( 1,9 ) - l n ( 1,8 ) 0,1 = 0,540672

D h f 1,8 = 0,540672

Passo 3

O valor real da derivada é:     f ' 1,8 =   0,555554

O valor aproximado é:   D h f 1,8 = 0,540672

Podemos comparar com a fórmula do erro absoluto:

E A =     f ' x - D h f x = 0,555554 - 0,540672 = 0,014

Resposta

D h f 1,8 = 0,540672

E A = 0,014

Exercício Resolvido #2

Adaptado de “Derivação e Integração numérica- Professor Renan G. P. Soares “

Dado a função f x = l n ⁡ ( x ) , calcular a derivação numérica com a fórmula da diferença centrada para x = 1,8   e h = 0,1 . Além disso, considere o valor real da derivada obtido no ponto dado e compare com o valor obtido.

Passo 1

O exercício é o mesmo que o anterior, com a diferença que agora usamos a fórmula da diferença centrada. Mas, se vc não lembra, aí está o valor da derivada real no ponto dado.

f ' ( 1,8 ) = 1 1,8 = 0,555554

Passo 2

Agora, conseguimos encontrar a derivada pelo método das diferenças centrada, usando a fórmula dada:

D h f x = f x - h , x + h = f x + h - f x - h 2 h

Se x = 1,8 ; h = 0,1 :

D h f x = f x , x + h = f 1,8 + 0,1 - f ( 1,8 - 0,1 ) 2 . ( 0,1 )

D h f x = f x , x + h = l n ⁡ ( 1,9 ) - l n ( 1,7 ) 0,2 = 0,55613

D h f 1,8 = 0,55613

Passo 3

O valor real da derivada é:     f ' 1,8 =   0,555554

O valor aproximado é:   D h f 1,8 = 0,55613

Podemos comparar com a fórmula do erro absoluto:

E A =     f ' x - D h f x = 0,555554 - 0,55613 = 0,000575

Resposta

D h f 1,8 = 0,55613

E A = 0,000575

Exercício Resolvido #3

Adaptado de “Derivação e Integração numérica- Professor Renan G. P. Soares “

Dado a função f x = l n ⁡ ( x ) , calcular a derivação numérica com a fórmula da diferença inferior para x = 1,8   e h = 0,1 . Além disso, considere o valor real da derivada obtido no ponto dado e compare com o valor obtido.

Passo 1

O exercício é o mesmo que o anterior, com a diferença que agora usamos a fórmula da diferença centrada. Mas, se vc não lembra, aí está o valor da derivada real no ponto dado.

f ' ( 1,8 ) = 1 1,8 = 0,555554

Passo 2

Agora, conseguimos encontrar a derivada pelo método das diferenças inferior, usando a fórmula dada:

D h f x = f x , x - h = f x - f ( x - h ) h

Se x = 1,8 ; h = 0,1 :

D h f x = f x , x + h = f 1,8 - f ( 1,8 - 0,1 ) 0,1

D h f x = f x , x + h = l n ⁡ ( 1 , 8 ) - l n ( 1 , 7 ) 0,1 = 0 , 571587

D h f 1,8 = 0,5 71587

Passo 3

O valor real da derivada é:     f ' 1,8 =   0,555554

O valor aproximado é:   D h f 1,8 = 0,5 71587

Podemos comparar com a fórmula do erro absoluto:

E A =     f ' x - D h f x = 0,555554 - 0,5 71587 = 0,01 603

Resposta

D h f 1,8 = 0,5 71587

E A = 0,01 603

Exercício Resolvido #4

Autoria do Responde Aí

Nós estudamos diferenciação progressiva, regressiva e central de primeira ordem. Existe diferenciação de outras ordens?

Passo 1

Progressiva de ordem 2 ou segunda ordem:

D 2 h f x = f x - 2 f x + h + f ( x + 2 h ) h 2

Passo 2

Regressiva de ordem 2:

D 2 h f x = f x - 2 h - 2 f x - h - f ( x ) h 2

Passo 3

Central de ordem 2:

D 2 h f x = f x - h - 2 f x + f ( x + h ) h 2

Resposta

Ei, a resposta está no passo a passo :)

Exercício Resolvido #5

Adaptado de REAMAT : Cálculo numérico 8.1 – Diferenciação numérica

Dado a função f x = e - x , calcular a derivação numérica para x = 1   e h = 0 , 0 1 . Calcular para diferenciação progressiva, regressiva e centrada.

Passo 1

Para diferenciação progressiva:

D h f x = f x , x + h = f x + h - f ( x ) h

Para x = 1   e h = 0,01 :

D h f x = f 1 + 0,01 - f ( 1 ) 0,01

D h f x = f 1,01 - f ( 1 ) 0,01

D h f x = e - 1,01 - e - 1 0,01 = - 0,36605

Passo 2

Para diferenciação regressiva:

D h f x = f x , x + h = f x - f ( x - h ) h

Para x = 1   e h = 0,01 :

D h f x = f 1 - f ( 1 - 0,01 ) 0,01

D h f x = f 1 - f ( 0,99 ) 0,01

D h f x = e - 1 - e - 0,99 0,01 = - 0,36 971

Passo 3

Para diferenciação centrada:

D h f x = f x + h - f ( x - h ) h

Para x = 1   e h = 0,01 :

D h f x = f 1 + 0,01 - f ( 1 - 0,01 ) 0,01

D h f x = f 1,01 - f ( 0,99 ) 0,01

D h f x = e - 1,01 - e - 0,99 0,01 = - 0,36788

Resposta

P r o g r e s s i v a → D h f x = - 0 , 36605

R e g r e s s i v a → D h f x = - 0 , 36 971

P r o g r e s s i v a → D h f x = - 0 , 36 788

Exercício Resolvido #6

Adaptado de REAMAT : Cálculo numérico 8.1 – Diferenciação numérica

Repita o exercício anterior para x = 1   e h = 0,01 .

Passo 1

Para diferenciação progressiva:

D h f x = f x , x + h = f x + h - f ( x ) h

Para x = 1   e h = 0,0 0 1 :

D h f x = f 1 + 0,0 0 1 - f ( 1 ) 0,0 0 1

D h f x = f 1,0 0 1 - f ( 1 ) 0,0 0 1

D h f x = e - 1,0 0 1 - e - 1 0,0 0 1 = - 0,3 6788

Passo 2

Para diferenciação regressiva:

D h f x = f x , x + h = f x - f ( x - h ) h

Para x = 1   e h = 0 , 0 01 :

D h f x = f 1 - f ( 1 - 0,0 0 1 ) 0,0 0 1

D h f x = f 1 - f ( 0,99 9 ) 0,0 0 1

D h f x = e - 1 - e - 0,99 9 0,0 0 1 = - 0,36 806

Passo 3

Para diferenciação centrada:

D h f x = f x + h - f ( x - h ) h

Para x = 1   e h = 0,0 0 1 :

D h f x = f 1 + 0,0 0 1 - f ( 1 - 0,0 0 1 ) 0,01

D h f x = f 1,0 0 1 - f ( 0,9 9 9 ) 0,0 0 1

D h f x = e - 1,0 0 1 - e - 0,9 9 9 0,0 0 1 = - 0,36788

Resposta

P r o g r e s s i v a → D h f x = - 0 , 36 788

R e g r e s s i v a → D h f x = - 0 , 36 806

P r o g r e s s i v a → D h f x = - 0 , 36788

Exercício Resolvido #7

Autoria do Responde aí

Considerando que um código computacional é muito importante para a resolução de problemas numéricos, defina as entradas e saídas para a implementação de um código de diferenciação numérica.

Passo 1

Entradas: x   e   h iniciais, função f ( x ) e função f ( x ± h ) .

Passo 2

Saída: o valor da derivada f ' ( x ) .

Resposta

Ei, a resposta está no passo a passo :)

Exercício Resolvido #8

Autoria do responde aí, com imagens obtidas do canal Matemática Base

Analise os gráficos a seguir e defina se pertence a A)Diferenciação progressiva; B) Diferenciação central ou C)Diferenciação regressiva.

( )

( )

( )

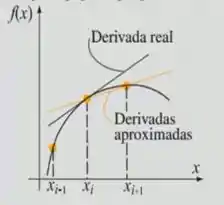
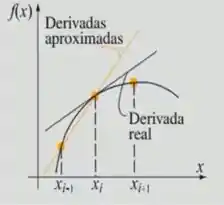
Passo 1

( A )

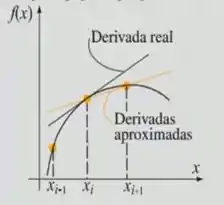
Observe que a reta traçada está acima da função, logo, a derivada é progressiva. Além disso, a reta pega os dois últimos pontos da curva.

Passo 2

( C )

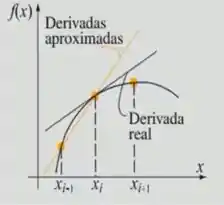
Perceba que essa reta pega apenas os dois primeiros pontos da curva, e é portanto, regressiva.

Passo 3

( B )

Perceba que agora, a reta intercepta o primeiro e ultimo ponto. É portanto, uma diferenciação centrada.

Resposta

( A )

( C )

( B )

Exercício Resolvido #9

Adaptado de Capítulo 21- Integração e diferenciação numérica (Unicamp)

Marque V para verdadeiro e F para falso:

( ) Pode ser utilizada para calcular a derivada aproximada a partir de dados tabulados que descrevem certa função.

( ) Comparado o resultado obtido com o da aproximação polinomial, observamos como a aproximação por diferenças finitas pode ser ruim (principalmente quando os dados são experimentais) .

( ) A diferenciação representa a inclinação de uma função.

( ) Diferenciação é muito mais sensível a alterações, ainda que pequenas, na função.

Passo 1

T o d a s   V e r d a d e i r a s

Resposta

Ei, a resposta está no passo a passo :)

Exercício Resolvido #10

Adaptado de Capítulo 6- Derivação Numérica da UFRGS

Encontre o valor da derivada da função f x = e x utilizando a diferenciação progressiva para x = 1   e h = [ 0,4   ; 0,2 ; 0,1   ; 0,05 ] .

Passo 1

a)Para x = 1   e h = 0 , 4 :

D h f x = f x , x + h = f x + h - f ( x ) h

D h f x = f 1 + 0 , 4 - f ( 1 ) 0 , 4

D h f x = f 1 , 4 - f ( 1 ) 0 , 4

D h f x = e 1 , 4 - e 1 0 , 4 = 3,3423

Passo 2

b) Para x = 1   e h = 0 , 2 :

D h f x = f x , x + h = f x + h - f ( x ) h

D h f x = f 1 + 0 , 2 - f ( 1 ) 0 , 2

D h f x = f 1 , 2 - f ( 1 ) 0 , 2

D h f x = e 1 , 2 - e 1 0 , 2 = 3 , 0092

Passo 3

c) Para x = 1   e h = 0 , 1 :

D h f x = f x , x + h = f x + h - f ( x ) h

D h f x = f 1 + 0 , 1 - f ( 1 ) 0 , 1

D h f x = f 1 , 1 - f ( 1 ) 0 , 1

D h f x = e 1 , 1 - e 1 0 , 1 2,8588

Passo 4

c) Para x = 1   e h = 0 , 05 :

D h f x = f x , x + h = f x + h - f ( x ) h

D h f x = f 1 + 0 , 05 - f ( 1 ) 0 , 05

D h f x = f 1 , 05 - f ( 1 ) 0 , 05

D h f x = e 1 , 05 - e 1 0 , 05 2 , 7873

Resposta

a )   D h f x = 3,3423

b )   D h f x = 3,0092

c )   D h f x = 2,8588

d )   D h f x = 2,7873