Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Integração de Romberg

Ver Todos os Exercícios

Teoria

Introdução

Faaaaaaaaaaaaaaaaaala meu caro, tudo certinho?

Vimos até agora que podemos usar métodos numéricos para obter a solução de uma integral definida do tipo:

∫ a b f x d x

Costumamos fazer essa aproximação por partes, em pontos dentro do intervalo, e normalmente usando pontos com mesma distância entre si.

Talvez você se lembre dos assuntos passados, quando falamos dos métodos dos trapézios e método 1/3 de Simpson ...

Nãooooooooooo, não é desse tipo de Simpson que estamos falando hahahahha

Pois bem, quando usamos esses métodos comparativamente e usando a mesma quantidade de pontos, a precisão do método de Simpson acaba sendo maior que a do método dos trapézios. Até aí tudo suave né?

E onde é que entra o método de Romberg?

O tal do Romberg viu que poderia melhorar e aumentar a precisão da regra dos trapézios aplicando um negócio chamado “extrapolação para o limite” de Richardson... Maaaaaaaaaaaaas vamos focar no nosso coleguinha Romberg.

Como calcular

Basicamente o Método de Romberg consiste na sucessiva aplicação da extrapolação de Richardson à uma quadratura composta de maior exatidão.

A determinação da integral é dada por:

I ≅ ∫ a b f x d x = h k 2 [ f a + f b + 2 ∑ i = 1 2 k - 1 f ( a + i . h k ) ]

Onde:

h k = b - a 2 k - 1

Aqui, h k representa a amplitude entre cada subintervalo.

Quando k = 1 , o limite superior será igual a zero e não precisaremos usar outros termos.

A primeira coisa que iremos fazer para resolver a integral é definir uma nova notação:

R k , j

Onde:

k = 1,2 , … , n

j = 1,2 , … , k

Aí meus caros, temos que ter um valor inicial... certo?

Primeiro quando k = 1 :

R 1,1 = h k 2 f a + f b

Generalizando para k = 2,3 , … , n ficamos com:

R k , 1 = 1 2 [ R k - 1,1 + h k - 1 [ ∑ i = 1 2 k - 2 f ( a + 2 i - 1 h k ) ]

Para situações em que j > 2 :

R k , j = R k , j - 1 + R k , j - 1 - R k - 1 , j - 1 4 j - 1 - 1

Parece confuso? Mas calma... já vamos entender para que serve tudo isso:

E para isso, conseguimos construir uma tabela com a seguinte aparência:

Montamos esse modelo, dependendo do k e chegamos no onde queremos e na resposta certa quando o erro for:

E = R n , n - R n - 1 , n R n , n < ε

Agora, chega de papo furado e bora fazer exercícios pra fixar bem o conteúdo. Bora lá?

Como calcular

Exercícios Resolvidos

Exercício Resolvido #1

Adaptado de Aula 8, Integração Numérica da Estácio

Utilize o conteúdo aprendido para realizar o primeiro passo da Integração de de Romberg para obter uma aproximação para a integral abaixo com k = 1,2 , 3   .

I = ∫ 0 π s e n x d x

Passo 1

Vamos determinar os termos R k , 1 :

R k , 1 = 1 2 [ R k - 1,1 + h k - 1 [ ∑ i = 1 2 k - 2 f ( a + 2 i - 1 h k ) ]

R 1,1 = h k 2 f a + f b

Para k = 1 :

R 1,1 = ( b - a ) 2 f a + f b

R 1,1 = ( π - 0 ) 2 s e n ( π ) + s e n ( 0 )

R 1,1 = 0

Passo 2

Para k = 2 :

R k , 1 = 1 2 [ R k - 1,1 + h k - 1 [ ∑ i = 1 2 k - 2 f ( a + 2 i - 1 h k ) ]

R 2,1 = 1 2 [ R 1,1 + h 1 . f a + h 2 ]

h k = b - a 2 k - 1

h k = b - a 2

R 2,1 = 1 2 [ R 1,1 + b - a . f a + b - a 2 ]

R 2,1 = 1 2 [ 0 + π - 0 . s e n 0 + π - 0 2 ]

R 2,1 = 1 2 [ π . s e n π 2 ]

R 2,1 = π 2 = 1,5708

Passo 3

Para k = 3 consideramos :

R k , 1 = 1 2 [ R k - 1,1 + h k - 1 [ ∑ i = 1 2 k - 2 f ( a + 2 i - 1 h k ) ]

R 3 , 1 = 1 2 { R 2 , 1 + h 2 . [ f a + h 3 + f a + 3 . h 3 ]

R 3,1 = 1 2 { R 2,1 + h 2 . [ f a + h 3 + f a + 3 . h 3 ]

h 3 = b - a 2 k - 1 = b - a 4

R 3,1 = 1 2 { R 2,1 + b - a 2 . f a + b - a 4 + f a + 3 . b - a 4 }

R 3,1 = 1 2 { R 2,1 + π - 0 2 . f 0 + π - 0 4 + f 0 + 3 . π - 0 4 }

R 3,1 = 1 2 { R 2,1 + π - 0 2 . f 0 + π - 0 4 + f 0 + 3 . π - 0 4 }

R 3,1 = 1 2 { 1,5708 + π 2 . f π 4 + f 3 . π 4 }

R 3,1 = 1 2 { 1,5708 + π 2 . s e n π 4 + s e n 3 . π 4 }

R 3,1 = 1,8962

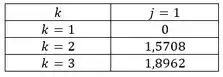
Resposta

Exercício Resolvido #2

Autoria do Responde Aí

A implementação do método de Romberg é muito importante para facilitar a resolução numérica de integrais.Defina as entradas necessárias para essa implementação numérica:

Passo 1

Para iniciar o programa, primeiro precisamos definir a função a ser implementada, os limites de integração e o número de iterações:

F=função a ser integrada

Xi=intervalo inicial de integração

Xf= intervalo final de integração

N= número de iterações

Resposta

F

Xi

Xf

N

Exercício Resolvido #3

Autoria do Responde Aí

Encontre o valor da integral abaixo com k = 1 :

∫ 0 1 e x 2 d x

Passo 1

Consideramos aqui f x = e x 2

A primeira coisa que faremos é calcular o passo h k : h k = b - a 2 k - 1

Se k = 1 ; a = 0   e   b = 1 :

h k = 1 - 0 2 1 - 1 = 1 1 = 1

Passo 2

Utilizando as fórmulas dadas k = 1 :

R 1,1 = h k 2 f a + f b

R 1,1 = 1 2 f 0 + f 1

R 1,1 = 1 2 f 0 + f 1

Se:

f x = e x 2

f 0 = e 0 = 1

f 1 = e 1 2 = e 1

R 1,1 = 1 2 1 + e 1 = 1,8591

Resposta

R 1,1 = 1 2 1 + e 1 = 1,8591

Exercício Resolvido #4

Adaptado de material “ejemplo del método de Romberg”

Encontre o valor da integral abaixo com k = 3 :

∫ 0 1 x 2 e - x d x

Passo 1

Aqui, levamos em consideração 3 subintervalos e então precisaremos dos seguintes termos conforme tabela:

Lembrando que toda fez que aparecer a notação f ( x ) aplicamos o valor usado como x na função f x = x 2 e - x

Passo 2

Agora, calculamos os valores de pontos para k = 1   e   j = 1 com base nas equações usadas no exercício 1:

R 1,1 = b - a 2 f a + f b

R 1,1 = 1 - 0 2 f 0 + f 1 = 0,1839

Para k = 2   e   j = 1 :

R 2,1 = 1 2 [ R 1,1 + b - a . f a + b - a 2 ]

R 2,1 = 1 2 [ 0,1839 + 1 - 0 . f 0 + 1 - 0 2 ]

R 2,1 = 1 2 0,1839 + . f 1 2 = 0,1678

Para k = 3   e   j = 1 :

R 3,1 = 1 2 { R 2,1 + a - b 2 . f a + a - b 4 + f a + 3 . a - b 4 }

R 3,1 = 1 2 { 0,1678 + 1 - 0 2 . f 0 + 1 - 0 4 + f 0 + 3 . 1 - 0 4 }

R 3,1 = 1 2 { 0,1678 + 1 2 . f 1 4 + f 3 . 1 4 = 0,1625

Passo 3

Agora calculamos a segunda coluna da tabela onde   j = 2 :

Para k = 2   e   j = 2 :

R k , j = R k , j - 1 + R k , j - 1 - R k - 1 , j - 1 4 j - 1 - 1

R 2 , 2 = R 2 , 1 + R 2 , 1 - R 1 , 1 4 2 - 1 - 1

R 2,2 = 0,1678 + 0,1678 - 0,1839 4 - 1 = 0,1624

Para k = 3   e   j = 2 :

R 3 , 2 = R 3 , 1 + R 3 , 1 - R 2,1 4 2 - 1 - 1

R 3,2 = 0,1625 + 0,1625 - 0,1624 4 - 1 = 0,1607

E por ultimo, calculamos para k = 3   e   j = 3

R 3,2 = R 3 , 2 + R 3 , 2 - R 2 , 2 4 3 - 1 - 1

R 3,2 = 0,1607 + 0,1607 - 0,1624 4 2 - 1 = 0,1606

Resposta

∫ 0 1 x 2 e - x d x = 0,1606

Exercício Resolvido #5

Autoria do Responde Aí

Para resolver uma integral qualquer em um dado intervalo, suponha que k = 10 quantos termos precisaríamos encontrar a resposta final da Integral definida?

Passo 1

Vamos montar a tabela dos termos calculáveis R de k , j . Considerando k = l i n h a s e j = c o l u n a s . Partindo do principio de que k = 10 , nosso j = 10 também. Então, podemos construir uma tabela 10x10.

Maaaaaaaaaas... nem todos os espaços da tabela podem ser preenchidos e nós os preenchemos gradativamente, conforme a coluna. Sempre o coeficiente k da linha é o mandante e os coeficientes j < k de cada coluna são apagados. Montamos uma tabela com essa aparência: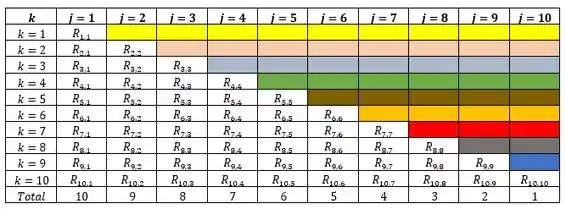

Somando tudo, temos 55 termos calculáveis até que possámos chegar na resposta R 10,10 .

Resposta

55 termos.

Exercício Resolvido #6

Lista 2 – UFRJ – Professor Daniel – Questão 8

O valor de π pode ser obtido através da resolução das seguintes equações: sin ⁡ x = 0 e cos ⁡ x + 1 = 0 . Aplique o Método de Newton-Raphson com x 0 = 3 e precisão 10 - 3 em cada caso e compare os resultados. Explique a diferença no número de iterações realizadas para atingir a precisão.

Passo 1

Cálculos Iniciais

f x = sin ⁡ x

f ' x = cos ⁡ x

g x = x - t g x

x 0 = 3

ε = 10 - 3

Iteração 1 :

x 1 = g x 0 = 3.14255

Critério de Parada:

x 1 - x 0 = 0.14255 > 10 - 3

Como não alcançamos o critério de parada continuamos as iterações.

x 1 = 3.14255

ε = 10 - 3

Iteração 2 :

x 2 = g x 1 = 3.14159

Critério de Parada:

x 2 - x 1 = 0.000954 < 10 - 3

Alcançamos nosso critério de parada. Então x - = 3.14159 .

Passo 2

Cálculos Iniciais

f x = 1 + cos ⁡ x

f ' x = - sin ⁡ x

g x = x + 1 + cos ⁡ x s i n x

x 0 = 3

ε = 10 - 3

Iteração 1 :

x 1 = g x 0 = 3.07091

Critério de Parada:

x 1 - x 0 = 0.07091 > 10 - 3

Como não alcançamos o critério de parada continuamos as iterações.

x 1 = 3.07091

ε = 10 - 3

Iteração 2 :

x 2 = g x 1 = 3.10627

Critério de Parada:

x 2 - x 1 = 0,03536 > 10 - 3

Como não alcançamos o critério de parada continuamos as iterações.

x 2 = 3.10627

ε = 10 - 3

Iteração 3 :

x 3 = g x 2 = 3.12393

Critério de Parada:

x 3 - x 2 = 0.01766 > 10 - 3

Como não alcançamos o critério de parada continuamos as iterações.

x 3 = 3.12393

ε = 10 - 3

Iteração 4 :

x 4 = g x 3 = 3.13276

Critério de Parada:

x 4 - x 3 = 0.00883 > 10 - 3

Como não alcançamos o critério de parada continuamos as iterações.

x 4 = 3.13276

ε = 10 - 3

Iteração 5 :

x 5 = g x 4 = 3.13718

Critério de Parada:

x 5 - x 4 = 0.00441 > 10 - 3

Como não alcançamos o critério de parada continuamos as iterações.

x 5 = 3.13718

ε = 10 - 3

Iteração 6 :

x 6 = g x 5 = 3.13939

Critério de Parada:

x 6 - x 5 = 0.00221 > 10 - 3

Como não alcançamos o critério de parada continuamos as iterações.

x 6 = 3.13939

ε = 10 - 3

Iteração 7 :

x 7 = g x 6 = 3.14049

Critério de Parada:

x 7 - x 6 = 0.0011 > 10 - 3

Como não alcançamos o critério de parada continuamos as iterações.

x 7 = 3.14049

ε = 10 - 3

Iteração 8 :

x 8 = g x 7 = 3.14104

Critério de Parada:

x 8 - x 7 = 0.00055 < 10 - 3

Alcançamos nosso critério de parada. Então x - = 3.14104 .

Passo 3

Po, na primeira tivemos que fazer só 2 iterações e na segunda 8 ! E não só isso, com aquelas 2 iterações conseguimos uma precisão MUITO maior do que com as 8 da segunda função. Por que isso? Cara, se liga, praticamente sempre que esse método demorar muito (tipo 8 iterações haha) é por causa daquele história da derivada!

Para f x = sin ⁡ x , temos f ' x = cos ⁡ x . No zero da função temos f ' π = - 1 , bem longe de zero.

Já para f x = 1 + cos ⁡ x , temos f ' x = - sin ⁡ x . No zero da função temos f ' π = 0 . E taí o motivo de demorar bem mais usando essa função ;)

Resposta

f x = sin ⁡ x : x - = 3.14159 ; 2 iterações.

f x = 1 + cos ⁡ x : x - = 3.14104 ; 8 iterações.

Na primeira função nós não só precisamos de bem menos iterações como também conseguimos uma precisão muito maior.

Isso acontece porque para a primeira função nós temos f ' π = - 1 . Já para a segunda nós temos f ' π = 0 . O fato de a derivada valer 0 na raiz da equação dificulta o método, fazendo com que ele precise de um número maior de iterações para obter uma precisão inferior.