Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Gregory Newton

Ver Todos os Exercícios

Teoria

Introdução

Fala meu jovenzito. Já estudamos até agora, alguns métodos diferentes para fazer a interpolação polinomial né?

E relembramos que valores igualmente espaçados (também chamados de nós) ...

Não esse tipo de nó... Hahahaha

Imagina que temos os seguintes pontos de uma função :

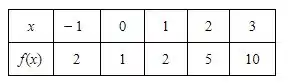
Percebe que os valores de x estão igualmente espaçados? A diferença deles nesse caso sempre é igual a 1.

Quando eles são igualmente espaçados, a fórmula de Newton pode ser simplificada, transformada na fórmula de Gregory-Newton.

Que cá entre nós, é só um nome chique para um caso particular do polinômio de Newton, pra pontos igualmente espaçados.

Forma de Newton-Gregory para o polinômio interpolador

Nós temos alguns pontos (os famigerados nós de interpolação) x 0 ,   x 1 ,   e   x n usaremos a fórmula de Newton-Gregory pra achar o polinômio interpolador p ( x ) , e esses pontos seguem um “passo” h . Isso significa que a cada passo x somamos h .

x k + 1 = x k + h

Na tabela anterior o passo h = 1 .

Moleza, né?

Existe um operador de diferença adiantada que é a diferença entre   f ( x   +   h ) - f ( x ) :

∆ 0 f ( x )   =   f ( x )  

∆ 1 f ( x )   =   f ( x   +   h ) - f ( x )  

∆ 2 f ( x )   =   ∆ ( ∆ f ( x ) )  

.   .   .  

∆ n f ( x )   =   ∆ ( ∆ ( n - 1 ) f ( x ) )

Para ficar mais simples de entender vamos montar uma tabela:

Vamos completar a tabela para o caso do exemplo de cima:

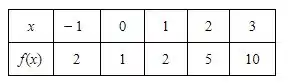
Fórmula de Gregory-Newton

Para montar o polinômio y 0 = P ( x 0 ) e com a notação dos deltas calculados anteriormente, ficamos com:

P n x = ∆ 0 f x + x - x 0 ∆ 1 f x 1 ! h 1 + x - x 0 x - x 1 ∆ 2 f x 2 ! h 2 + … … + x - x 0 x - x 1 … x - x n - 1 ∆ n f x n ! h n  

Pensando no exemplo anterior vamos encontrar o polinômio y 0 = P ( x 0 ) :

P n x = ∆ 0 f x + x - x 0 ∆ 1 f x 1 ! h 1 + x - x 0 x - x 1 ∆ 2 f x 2 ! h 2 + x - x 0 x - x 1 x - x 2 ∆ 3 f x 3 ! h 3

P n x = 2 + x - ( - 1 ) - 1 1 ! 1 1 + x - ( - 1 ) x - 0 2 2 ! 1 2 + x - ( - 1 ) x - 0 x - 1 0 3 ! 1 3

P n x = x ² + 1

Esse polinômio é empregado em diversos graus de complexidade. Bora calcular exercícios que esse é molezinha !!!!

Forma de Newton-Gregory para o polinômio interpolador

Fórmula de Gregory-Newton

Exercícios Resolvidos

Exercício Resolvido #1

Adaptado de Material Cáculo numérico do professor Anderson Vieira

Calcule até o segundo delta dos seguintes pontos, onde f ( x )   =   x , considerando os seguintes pontos e com h = 0,1 :

Passo 1

Inicialmente, vamos montar os deltas necessárias, onde:

Δ 0 f x = f x

Como h = 0,1

O primeiro delta é o valor da função aplicado nos pontos:

Então, basicamente é feito:

Δ 0 f 2 = f 2 =   2

Δ 0 f 2 , 1 = f 2,1 =   2,1

Δ 0 f 2 , 2 = f 2,2 =   2,2

Δ 0 f 2 , 3 = f 2,3 =   2,3

Δ 0 f 2 , 4 = f ( 2,4 )   =   2,4

Passo 2

O próximo delta usamos a seguinte fórmula: Δ 1 f x = f ( x + h ) - f x

Δ 1 f 2 = f 2 + 0,1 - f 2 = 0,034923

Δ 1 f 2,1 = f 2,1 + 0,1 - f 2,1 = 0,034102

Δ 1 f 2,2 = f 2,2 + 0,1 - f 2,2 = 0,033345

Δ 1 f 2,3 = f 2,3 + 0,1 - f 2,3 = 0,032618

Passo 3

Podemos agora, montar a tabela:

Resposta

Exercício Resolvido #2

Material adaptado do site Engenharia Mais Fácil

Construa e encontre o polinômio interpolador para a tabela abaixo:

Passo 1

Com esses dados, conseguimos construir outra tabela com valores para Δ y o , Δ y 1 e   Δ y 2 :

Passo 2

O polinômio interpolador é dado por:

P n x = a 0 + a 1 x - x 0 … a n ( x - x 0 ) ( x - x n - 1 )

Os termos a são dados por:

a 0 = y 0 = - 5

a 1 = 5

a 2 = - 4 2 ! 1 2 = - 2

a 3 = 6 3 ! 1 3 = 1

Passo 3

Podemos agora montar o polinômio:

P x = - 5 + 5 x - - 2 - 2 x - - 2 x - - 1 + 1 ( x - - 2 ) ( x - - 1 ) ( x - 0 )

P x = - 5 + 5 x + 2 - 2 x + 2 x + 1 + 1 x + 2 x + 1 x

P x = - 5 + 5 x + 10 - 2 x 2 - 2 x - 4 x - 4 + x 3 + x 2 + 2 x 2 + 2 x

∴

P x = x 3 + x 2 + x + 1

Resposta

P x = x 3 + x 2 + x + 1

Exercício Resolvido #3

Autoria e adaptação da apostila de cálculo numérico de Flávia Bastos

Calcular P 1 ( 0,2 ) usando os dados da tabela:

Passo 1

Analisando a tabela, vemos que x i - x f = h

0,6 - 0,1 = 0,5 = h

Com esse valor e fazendo algumas considerações:

s = x - x 0 h = 0,2 - 0,1 0,5 = 0,2

Consideramos aqui, n = 1 , já que temos dois termos e isso significa que temos apenas um nó entre eles!

Podemos agora, começar a montar o polinômio.

Passo 2

Agora, com essa fórmula nós montamos o polinômio interpolador:

P 1 x = y 0 + Δ y 0 s

P 1 0,2 = 1,221 + 2,099 * 0,2

P 1 0,2 = 1,641

Passo 3

Podemos verificar que:

P 1 x = y 0 + Δ y 0 s = y 0 + ( y 1 - y 0 ) x - x 0 x 1 - x 0

Resposta

P 1 0,2 = 1,641

Exercício Resolvido #4

Autoria e adaptação da apostila de cálculo numérico de Flávia Bastos

Calcular P 2 ( 115 ) usando os dados da tabela:

Passo 1

Analisando a tabela, vemos que x i - x f = h

110 - 120 = 10 = h

Com esse valor e fazendo algumas considerações:

s = x - x 0 h = 115 - 110 10 = 0,5

Consideramos aqui, n = 2 , já que temos três termos e isso significa que temos dois nós entre eles!

Podemos agora, começar a montar o polinômio.

Passo 2

Agora, com essa fórmula nós montamos o polinômio interpolador:

P 2 x = y 0 + Δ y 0 s + Δ 2 y 0 s 2 ! ( s - 1 )

P 2 115 = 2,041 + 0,038 * 0,50 - 0,003 2 ( 0,5 ) ( 0,5 - 1 )

P 2 115 = 2,060

Resposta

P 2 115 = 2,060

Exercício Resolvido #5

Autoria e adaptação da apostila de cálculo numérico de Flávia Bastos

Sabe-se que interpolar é fundamental para solucionar problemas, mas, quando temos problemas extensos é necessário o uso de ferramentas computacionais para tornar os problemas mais ~solucionáveis’’ .Defina o objetivo, as entradas e saídas para o polinômio interpolador de Newton-Gregory!

Passo 1

Objetivo: O algoritmo serve para interpolar o valor utilizando o polinômio de Gregory-Newton.

Passo 2

Os parâmetros de entrada são o número ( n )   de incógnitas, e as variáveis x ,   y ,   z até a quantidade necessária.

Passo 3

O parâmetro de saída necessário é o valor ( f ) interpolado.

Resposta

Objetivo: Utilizar o polinômio.

Entradas: n ,   x ,   y ,   z .

Saída:   f .