Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Ruggiero - Aspectos Teóricos e Computacionais- Ed: 2º - Capítulo 8.Exercícios - Ex. 22

  1. Apresente a fórmula de iteração para o método de Taylor de· ordem 2 aplicado ao PVI abaixo:

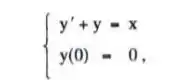
sendo h = 0.1;

  1. verifique que y(x) = exp(-x) + x - 1 é solução do PVl;
  2. calcule um limitante superior para o erro do método obtido em (a).

Passo 1

Letra a:

Aqui nem temos que fazer tantas contas assim! Ele só nos pediu uma fórmula de iteração!

Lembrando que no caso geral ela é:

y n + 1 = y n + y ' n h + y ' ' n 2 h 2

Vamos calcular as derivadas necessárias:

y ' n = x n - y n

y ' ' = 1 - y '

y ' ' n = 1 - y ' n = 1 - ( x n - y n ) = y n - x n + 1

Daí, a fórmula de iteração fica:

y n + 1 = y n + 0.1 ( x n - y n ) + 0.005 ( y n - x n + 1 ) = 0.905 y n + 0.095 x n + 0.005

Passo 2

Letra b:

Primeiro fazemos:

y ( 0 ) = e 0 + 0 - 1 = 1 - 1 = 0 .

Agora, temos que calcular y ' ( x ) :

y ' ( x ) =   - e - x + 1

Substituindo:

- e x + 1 + e - x + x - 1 = x = 0

y ( x ) = e - x + x - 1 é solução.

Passo 3

Letra c:

O erro de truncamento é dado por:

| E | ≤ y 3 6 Ξ h 3 = 1 0 - 3 6 y 3 Ξ

Precisamos achar Ξ que maximize y 3 .

Como essa função é sempre crescente, temos que o valor será limitado por:

| E | ≤ 1 0 - 3 6 y ' ' ( X n )

Resposta

  1. y n + 1 = 0.905 y n + 0.095 x n + 0.005
  2. y ( x ) = e - x + x - 1 é solução.
  3. | E | ≤ 1 0 - 3 6 y ' ' ( X n )
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

23. Considere a equação diferencial y ' = y sen ⁡ y + x com a condição inicial y 0 = 1 . Calcule y ' ( 0 ) , y ' ' ( 0 ) e y ' ' ' ( 0 ) . Utilizando esta informação calcule aproximadamente y ( 0.2 )