Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Ruggiero - Aspectos Teóricos e Computacionais- Ed: 2º - Capítulo 8.Exercícios - Ex. 9

9. Dado o PVI y ' = - x y , y 0 = 20 , deseja-se encontrar uma aproximação para y ( 16 ) . Resolva por

a) Runge-Kutta de 2 ª ordem, h = 2

b) Runge-Kutta de 4 ª ordem, h = 4

c) O par previsor-corretor do texto

d) Comente seus resultados

Passo 1

a) Vamos começar usando o método de Runge-Kutta de 2 ª ordem, h = 2 ...

Só que o método de Runge-Kutta de 2 ª ordem é nada mais do que o método de Euler melhorado. Desse modo, usando a já conhecida fórmula de recorrência abaixo...

y n + 1 = y n + h 2 [ f x n , y n + f ( x n + 1 , y n + 1 ) ]

Chamando y ' de f ( x n , y n ) , então...

y n + 1 = y n + h 2 - x n y n + x n + 1 y n + 1

y n + 1 = y n + h 2 - n h y n - n + 1 h y n - n h y n

Passo 2

Vamos resolver isso computacionalmente!

Afinal se fosse fazer aqui, seriam precisos um número de iterações igual a...

n í m e r o   d e   i t e r a ç õ e s = 16 - 0 2 = 8

Então bora resolver computacionalmente! Usando o seguinte código abaixo...

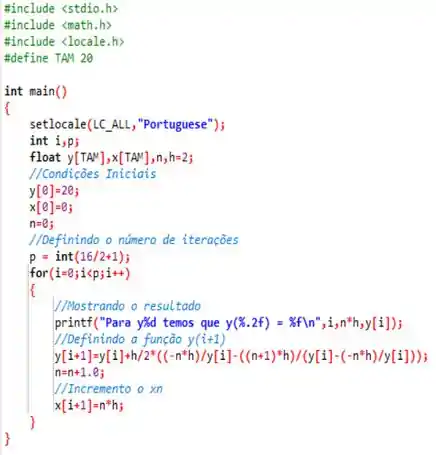
Passo 3

b) Se liga só! Agora vamos usar o método de Runge-Kutta de 4 ª ordem pra resolver essa equação...

A fórmula de recorrência do método de Runge-Kutta de 4 ª ordem é dada por...

y n + 1 = 1 6 ( k 1 n + 2 k 2 n + 2 k 3 n + k 4 n )

Sendo assim, chamando y ' d e f x n , y n , temos para k 1 n

  k 1 ( n ) = h f ( x n , y n )

k 1 n = - n h y n

k 2 n = h f x n + h 2 , y n + k 1 ( n ) 2

k 2 n = - n h + h 2 y n + k 1 ( n ) 2

k 3 n = h f x n + h 2 , y n + k 2 n 2

k 3 n = h - n h + h 2 y n + k 2 n 2

k 4 n = h f x n + h 2 , y n + k 3 n 2

k 4 n = h - n h + h 2 y n + k 3 n 2

Desse modo, utilizando o seguinte código confeccionado abaixo...

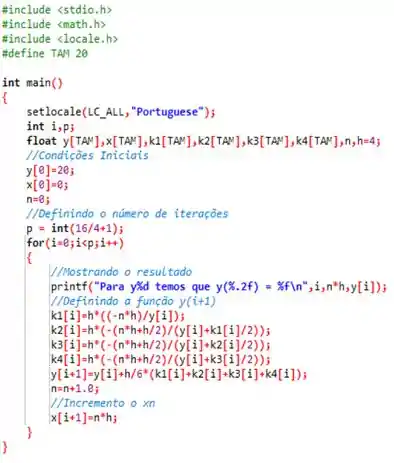
Obtemos o seguinte resultado para y ( 16 ) ...

y 16 ≅ 11.998

Passo 4

c) A bola da vez agora é o método preditor-corretor...

Usando o modelo Adams-Moulton-Bashfort podemos gerar um método de três passos com essa aparência:

y 0 = α 0

y 1 = α 1

y 2 = α 2

Para o método preditor, temos que...

y n + 1 p = y n + h 12 ( 23 f n - 16 f n - 1 + 5 f n - 2 )

Já para o método corretor...

y n + 1 = y n + h 24 ( 9 f n + 1 p + 19 f n - 5 f n - 1 + f n - 2 )

Fazendo as nossa iterações, obtemos então que para h = 2 ...

y 16 ≅ 11.99199

E para h = 4 ...

y ( 16 ) ≅ 11.94514

Resposta

a) P a r a   h = 2 → y 16 ≅ 12,00999

b)

P a r a   h = 2 → y 16 ≅ 11.998

c)

P a r a   h = 2 → y 16 ≅ 11.99199

P a r a   h = 4 → y ( 16 ) ≅ 11.94514

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

5.Considere os métodos ( 3 ) do texto. Faça m = 3 e p = 3 e deduza o método bem como a expressão do erro.