Muitas equações de estado foram desenvolvidas para descrever as relações entre pressão, , volume molar, , e temperatura, , de gases. Uma das equações mais utilizadas é equação de Beattie-Bridgeman:
onde é a constante universal dos gases e são parâmetros característicos do gás em estudo. O segundo, terceiro e quarto termos de , podem ser vistos como correções da lei dos gases ideais, , para o comportamento não ideal de um gás. Os parâmetros são definidos por:
onde: são constantes determinadas experimentalmente e são diferentes para cada gás. Dados os valores de pressão, , temperatura, , e das constantes é poss´ıvel determinar o volume molar de qualquer gás resolvendo a equação , usando como estimativa inicial para o volume molar a lei dos gases ideais: . Para o gás metano, tem-se que: . Considere temperaturas de e as seguintes preções em . Com esses dados, determine:
a) o volume molar do gás metano, com precisão de
b) o fator de compressibilidade , onde ;
c) compare os seus resultados com valores experimentais do fator de compressibilidade para o metano de , apresentados na Figura :
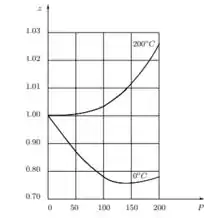
Passo 1
Falaaaaa rapaziada tudo blz?
Nessa questão do livro de cálculo numérico de Franco e Neide sabendo que muitas equações de estado foram desenvolvidas para descrever as relações entre pressão, , volume molar, , e temperatura, , de gases. Uma das equações mais utilizadas é equação de Beattie-Bridgeman:
onde é a constante universal dos gases e são parâmetros característicos do gás em estudo. O segundo, terceiro e quarto termos de , podem ser vistos como correções da lei dos gases ideais, , para o comportamento não ideal de um gás. Os parâmetros são definidos por:
onde: são constantes determinadas experimentalmente e são diferentes para cada gás. Dados os valores de pressão, , temperatura, , e das constantes é poss´ıvel determinar o volume molar de qualquer gás resolvendo a equação , usando como estimativa inicial para o volume molar a lei dos gases ideais: . Para o gás metano, tem-se que: . Considere temperaturas de e as seguintes preções em . Com esses dados, determine:
a) o volume molar do gás metano, com precisão de
b) o fator de compressibilidade , onde ;
c) compare os seus resultados com valores experimentais do fator de compressibilidade para o metano de , apresentados na Figura :
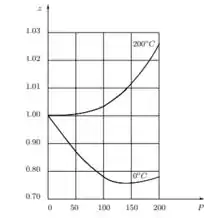

Precisa ficar assim não meus abençoados conforme você for vendo os passos vai perceber que ela é de boa.
Passo 2
Então galerinha na letra (a) para determinarmos o volume molar do gás metano com pressão de temos,
Ficando,
Já na letra (b) para o fator de compressibilidade ,
E por fim na letra comparando os valores obtidos no gráfico dado no passo anterior temos,
Espero que eu tenha ajudado e te vejo no próximo desafio.
Até a próxima.

Resposta
a)
b)
c)