Considere um circuito de polarização que consiste de uma bateria com uma tensão e um resistor em série, conectado a um diodo semicondutor de estado sólido como mostrado na Figura .

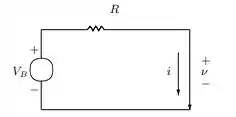
As características operacionais na gama normal de operação de um diodo são determinadas pela equação relacionando suas variáveis terminais de tensão e corrente. Se tomarmos como sendo estas variáveis e escolhermos as direções de referência relativas mostradas, a equação relacionando estas variáveis é dada por:

onde:

é a intensidade de corrente de saturação reversa. Esta é a corrente máxima que flui quando o diodo é polarizado em reverso, ou seja, quando . Ela é função do material usado na confecção do diodo, do grau de lubrificação e das técnicas de fabricação particulares. Um valor típico para um diodo de silício em temperatura ambiente é Ampére;

é a constante de Boltzmann, que tem o valor: ;

é a temperatura absoluta em na qual o diodo é operado;

é a carga do elétron que tem o valor:

Em temperaturas ambientes normais, o valor do termo é aproximadamente . Podemos agora proceder à solução do circuito de polarização, ou seja, encontrar os valores de . Para isso, basta aplicar a lei das tensões de Kirchoff ao circuito, obtendo assim:

Falaaaaa rapaziada tudo blz?

Nessa questão do livro de cálculo numérico de Franco e Neide considerando um circuito de polarização que consiste de uma bateria com uma tensão e um resistor em série, conectado a um diodo semicondutor de estado sólido como mostrado na Figura .

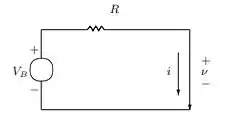
As características operacionais na gama normal de operação de um diodo são determinadas pela equação relacionando suas variáveis terminais de tensão e corrente. Se tomarmos como sendo estas variáveis e escolhermos as direções de referência relativas mostradas, a equação relacionando estas variáveis é dada por:

onde:

é a intensidade de corrente de saturação reversa. Esta é a corrente máxima que flui quando o diodo é polarizado em reverso, ou seja, quando . Ela é função do material usado na confecção do diodo, do grau de lubrificação e das técnicas de fabricação particulares. Um valor típico para um diodo de silício em temperatura ambiente é Ampére;

é a constante de Boltzmann, que tem o valor: ;

é a temperatura absoluta em na qual o diodo é operado;

é a carga do elétron que tem o valor:

Em temperaturas ambientes normais, o valor do termo é aproximadamente . Podemos agora proceder à solução do circuito de polarização, ou seja, encontrar os valores de . Para isso, basta aplicar a lei das tensões de Kirchoff ao circuito, obtendo assim:

Precisa ficar assim não meus abençoados conforme você for vendo os passos vai perceber que ela é de boa.