Num escoamento turbulento em uma rede de tubulação interconectada, a razão de escoamento de um nós. Para outro é proporcional à raiz quadrada da diferença entre as pressões nos nós. Para a rede da figura a seguir é solicitado determinar a pressão em cada nó.

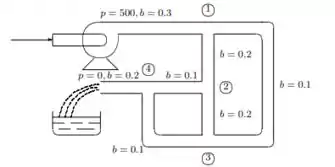
Os valores de representam fatores de condutância na relação:

As equações para as pressões em cada nó são então dadas por:

onde estamos assumindo que ; se isso não for verdadeiro é necessário modificar as equações. Resolva o sistema dado pelo método de Newton

Falaaaaa rapaziada tudo blz?

Nessa questão do livro de cálculo numérico de Franco e Neide um escoamento turbulento em uma rede de tubulação interconectada, a razão de escoamento de um nós. Para outro é proporcional à raiz quadrada da diferença entre as pressões nos nós. Para a rede da figura a seguir é solicitado determinar a pressão em cada nó.

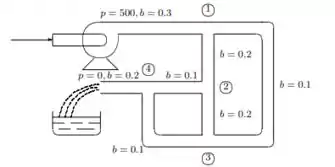
Os valores de representam fatores de condutância na relação:

As equações para as pressões em cada nó são então dadas por:

onde estamos assumindo que ; se isso não for verdadeiro é necessário modificar as equações. Resolva o sistema dado pelo método de Newton

Precisa ficar assim não meus abençoados conforme você for vendo os passos vai perceber que ela é de boa.