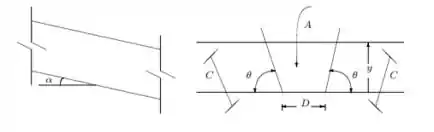
A Figura abaixo representa o fluxo de água em um canal aberto:Uma relação empírica para o fluxo é a equação de Chez-Manning: Q = 1,49 E A R 2 3 S 1 2 Onde: • Q -f l u x oe m m 3 s e g . ; • E - c o e f i c i e n t ed ea t r i t od e t e r m i n a d oe x p e r i m e n t a l m e n t e ,v a l e n d oe n t r e0,025e 0,035p a r aam a i o r i ad o sc a n a i ser i o s ; •A-á r e ad as e c ç ã ot r a n s v e r s a ld oc a n a l ; á çã •R-r a i oh i d r á u l i c oq u eéd e f i n i d oc o m oar a z ã oe n t r eaá r e aAeop e r í m e t r o2C+D ; á é ã á í •α-i n c l i n a ç ã od oc a n a l( S=s e nα ) . çã a) Para um canal retangular ( θ=90 ° ) , sendo conhecidos Q ,E , S ,D , verificar que y é a solução da equação: 1,49 E 3 D 5 S 1 2 y 5 - 4 Q 3 y 2 - 4 Q 3 D y - Q 3 D 3 = 0 , Em qual tem apenas uma raiz positiva.b) Encontre as profundidades y do canal correspondente a duas estações AeB , cujos dados estão tabelados a seguir:Em cada caso determinar incialmente intervalo contendo a raiz.

a) 3,92x10 9y 5 - 9,41x10 6y 2 - 1,88x10 8y - 9,41x10 8 b) 2,44x10 8e - 3.92x10 - 7

Enunciado

Falaaaaa rapaziada tudo blz?

Nessa questão do livro de cálculo numérico de Franco dado uma figura que representa o fluxo de água em um canal aberto:

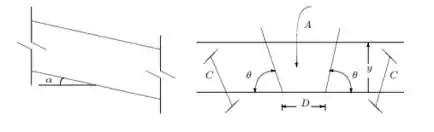
Uma relação empírica para o fluxo é a equação de Chez-Manning:

Onde:

a) Para um canal retangular , sendo conhecidos verificar que y é a solução da equação:

Em qual tem apenas uma raiz positiva.

b) Encontre as profundidades y do canal correspondente a duas estações , cujos dados estão tabelados a seguir:

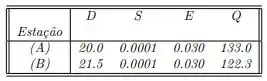
Em cada caso determinar incialmente intervalo contendo a raiz.

Precisa ficar assim não meus abençoados conforme você for vendo os passos vai perceber que ela é de boa.

Então galera na letra (a) ele pede para determinarmos a equação,

Dado que na estação (a) temos,

Ficando,

Temos,

Já na letra (b) para determinar as profundidades do canal correspondente a , dado

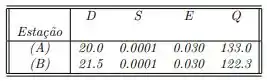
Temos,

Ficando,

E para exportação (b) temos,

Espero que eu tenha ajudado e te vejo no próximo desafio.

Até a próxima.