Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Franco e Neide B - Cálculo Numérico- Ed: 1º - Capítulo 11.Exercícios - Ex. 8

Usando a regra (1)/(3) de Simpson, calcular:

Sabe-se que:

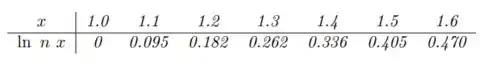
Passo 1

Salve meu colega! Tudo na paz? Vamos usar novamente a regra (1)/(3) de Simpson, sendo que a mesma em sua forma simples é dada por:

(h)/(3) (𝑦 0 + 4 𝑦 1 + 𝑦 2)

Porém como temos vários pontos, teremos que mexer um pouco na fórmula, visto que temos que formar os intervalos. Fazendo as alterações necessárias e considerando que os valores de l n l n (𝑥) dados na tabela correspondem a y0, y1, y2 ... até y6, obtemos:

(h)/(3) (𝑦 0 + 4 𝑦 1 + 𝑦 2) + (h)/(3) (𝑦 2 + 4 𝑦 3 + 𝑦 4) + (h)/(3) (𝑦 4 + 4 𝑦 5 + 𝑦 6)

Simplificando:

(h)/(3) (𝑦 0 + 4 𝑦 1 + 2 𝑦 2 + 4 𝑦 3 + 2 𝑦 4 + 4 𝑦 5 + 𝑦 6)

Passo 2

Agora só basta substituir os valores e calcular o resultado. Primeiramente vamos calcular o passo (h) que é dado por h = (1.6 - 1)/(6) = 0.1 :

(0.1)/(3) (0 + 4 (0.095) + 2 (0.182) + 4 (0.262) + 2 (0.336) + 4 (0.405) + 0.470) = 0.1518

Prontinho! Integral calculada.

Resposta

O valor da integral foi aproximadamente 0.1518 .

Exercícios de Livros Relacionados

Estime o número mínimo de subintervalos necessários para aproximar a integral: ∫ 1 2 x d x com um erro de magnitude inferior a 10 - 4 através da:Regra do trapézioRegra de Simpson
Estime o número mínimo de subintervalos necessários para aproximar a integral: ∫ 0 2 sen ⁡ ( x + 1 ) d x com um erro de magnitude inferior a 10 - 4 através da:Regra do trapézioRegra de Simpson
Estime o número mínimo de subintervalos necessários para aproximar a integral: ∫ 2 4 1 ( s - 1 ) 2 d s com um erro de magnitude inferior a 10 - 4 através da:Regra do trapézioRegra de Simpson
Estime o número mínimo de subintervalos necessários para aproximar a integral: ∫ 0 3 x + 1 d x com um erro de magnitude inferior a 10 - 4 através da:Regra do trapézioRegra de Simpson
Estime o número mínimo de subintervalos necessários para aproximar a integral: ∫ - 1 1 ( t 3 + 1 ) d t com um erro de magnitude inferior a 10 - 4 através da:Regra do trapézioRegra de Simpson