Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Franco e Neide B - Cálculo Numérico- Ed: 1º - Capítulo 11.Exercícios - Ex. 15a

Calcular:

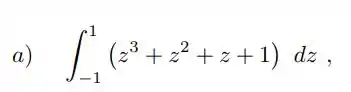
Por quadratura de Gauss e diretamente e comparar os resultados.

Passo 1

Eaii! Tudo belezinha? No exercício proposto, temos uma integral definida que vai de –1 até 1, que é uma das condições para usarmos a quadratura de Gauss. Caso você não se lembre, a quadratura de Gauss pode ser feita seguindo a relação a seguir:

∫ 𝑎 𝑏 𝑓 𝑥 𝑑 𝑥 = ∫ − 1 1 𝑓 𝑥 𝑡 𝑏 − 𝑎 2 𝑑 𝑡

Tal relação é utilizada para a quadratura de Gauss de 2 pontos. Como já temos o intervalo de − 1   até 1   , iremos apenas resolver a integral:

∫ − 1 1 𝑧 3 + 𝑧 2 + 𝑧 + 1   𝑑 𝑧   =   𝑧 4 4 + 𝑧 3 3 + 𝑧 2 2 + 𝑧 − 1     1

Resolvendo chegamos em:

  𝑧 4 4 + 𝑧 3 3 + 𝑧 2 2 + 𝑧 − 1     1   =   2.6666 …

Resposta

O resultado da integral é   2.6666 …  

Exercícios de Livros Relacionados

Deduza a fórmula de integração da forma ∫ - 1 1 f ( x ) d x ≈ w 0 f ( - 0.5 ) + w 1 f ( 0 ) + w 2 f ( 0.5 ) que integre exatamente polinômios de grau ≤ 2.
Calcular:Por quadratura de Gauss e diretamente e comparar os resultados.
Escolha uma regra de quadratura sobre pontos igualmente espaçados de h e avalie: ∫ − 1 0 𝑥 𝑒 𝑥 𝑑 𝑥 ,Com duas casas decimais corretas.